Перпендикулярность прямой и плоскости

Урок 19. Перпендикулярность прямой и плоскости.

Решите задачу.

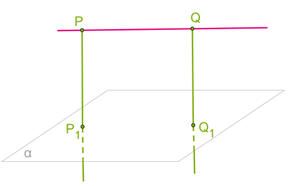
Прямая PQ параллельна плоскости α.

От точек P и Q к плоскости проведены прямые PP1⊥ α и QQ1⊥ α. Известно, что PQ=PP1=2, 8 см.

Определи вид четырёхугольника PP1Q1Q и найди его периметр.

Ответ:

1. PP1Q1Q —;

2. PPP1Q1Q= см.

Для решения задачи прочитайте теорию.

Перпендикулярность прямой и плоскости

Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости.

Перпендикулярность прямой и плоскости обозначается как a⊥ α.

Через любую точку пространства перпендикулярно данной плоскости проходит прямая, притом только одна.

Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости.

1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

2. Две прямые, перпендикулярные одной и той же плоскости, параллельны.