
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теоремой, обратной к данной, называется такая теорема, в которой условие и заключение поменяли местами.
Тема урока: Аксиома параллельных прямых. 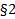 стр. 57.
стр. 57.
Видеоурок https: //www. youtube. com/watch? v=F1g24WI7A-k
Записываем, в тетрадь то, что выделено синим и решение задач.
Двадцать шестое января
Классная работа
Аксиома параллельных прямых. Свойства параллельных прямых.
Сегодня мы познакомимся с понятиями аксиома. Изучим следствия из аксиомы о параллельных прямых.
Изучим свойства параллельных прямых. Научимся формулировать теорему, обратную данной.
Познакомимся со способом доказательства от противного.
Запомните!
Аксиома (от др. греческого ( axioma ) — значимое, принятое положение) — это правило, которое считается верным без необходимости представления доказательств.
Или проще:
Аксиома — утверждение, которое не требует доказательств.
Синоним аксиомы — постулат. Антоним — гипотеза-.
Аксиома параллельных прямых:
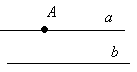
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия:
1) Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
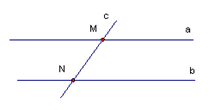
2) Две прямые, параллельные третьей, параллельны между собой.

Теоремой, обратной к данной, называется такая теорема, в которой условие и заключение поменяли местами.
Разберем на примере изученных теорем о накрест лежащих, односторонних и соответственных углах.
|
Свойства параллельных прямых. Уже изучены. |
Признаки параллельных прямых (обратные теоремы). Изучаем | ||
| Условие теоремы | Заключение теоремы | Условие теоремы | Заключение теоремы |
| 1. Если накрест лежащие углы равны, то |  b b
| 1. Если 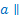 b, то b, то
| Накрест лежащие углы равны. |
| 1. Если соответственные углы равны, то | 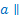 b b
| 1. Если 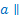 b, то b, то
| Соответственные углы равны |
1. Если сумма односторонних углов 180 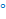 , то , то
| 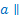 b b
| 1. Если 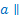 b, то b, то
| Сумма односторонних углов 180 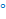
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|