Дистанционное обучение. Урок «Наибольшее и наименьшее значения функции». Наибольшее и наименьшее значения функции на отрезке

Дистанционное обучение

Урок «Наибольшее и наименьшее значения функции»

Цели: изучить понятия наибольшее и наименьшее значения функции; наибольшее и наименьшее значения функции на отрезке; формирование навыков в исследовании функции с помощью производной.

Устно. №936

Контрольные вопросы:

1. Всегда ли наибольшее и наименьшее значения функции находятся в точках экстремума?

2. В чем отличие между экстремумами функции и, наибольшим и наименьшим, значениями функции?

Наибольшее и наименьшее значения функции на отрезке

Свои наибольшее и наименьшее значения на отрезке функция принимает либо на концах данного отрезка, либо в стационарных точках (т. е. в точках, в которых производная равна нулю 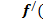x )=0), принадлежащих этому отрезку.

Алгоритм:

1. Найти производную функции .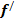

2. Найти стационарные точки 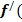x )=0.

3. Проверить, принадлежат ли стационарные точки заданному отрезку.

4. Найти значения функции на концах отрезка.

5. Найти значения функции в стационарных точках, принадлежащих этому отрезку.

6. Выбрать из всех найденных значений наибольшее и наименьшее.

Записать ответ .

Пример 1

Найти наибольшее и наименьшее значения функции 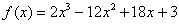на отрезке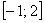

Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:

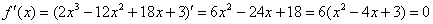
Полученное квадратное уравнение имеет два действительных корня:
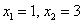– критические точки.

Ещё раз подчёркиваю, что нас не интересует, есть в них максимумы/минимумы или нет.

Первая критическая точка принадлежит данному отрезку: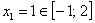
А вот вторая – нет: 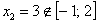, поэтому про неё сразу забываем.

Вычислим значение функции в нужной точке:

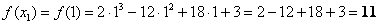
Итоговый результат я выделила жирным цветом, при оформлении задания в тетради его удобно обвести в кружок простым карандашом или пометить как-то по-другому.

2) Вычислим значения функции на концах отрезка:

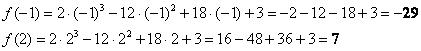
Результаты опять каким-либо образом выделяем.

3) Дело сделано, среди «жирных» чисел выбираем наибольшее и наименьшее.

Ответ: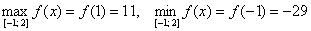

Решение задач №936, 937, 938, 939 (учебник)