
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
функция R является нечетной относительно cosx.
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
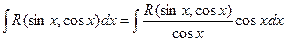
Функция 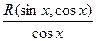 может содержать cosx только в четных степенях, а, следовательно, может быть преобразована в рациональную функцию относительно sinx.
может содержать cosx только в четных степенях, а, следовательно, может быть преобразована в рациональную функцию относительно sinx.
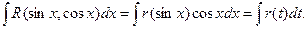
Пример. 
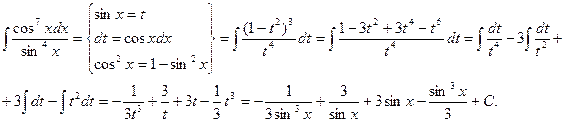
Для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл вида если
функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда 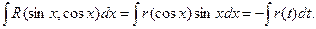
Интеграл вида 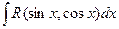
функция R четная относительно sinx и cosx.
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Тогда 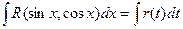
Пример. 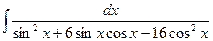

Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
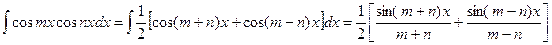
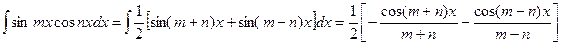
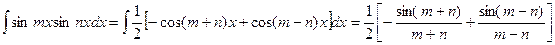
Пример. 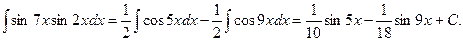
Интегрирование некоторых иррациональных функций
Интеграл вида где n- натуральное число.
С помощью подстановки 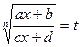 функция рационализируется.
функция рационализируется.
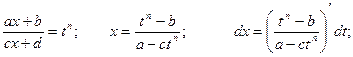
Тогда 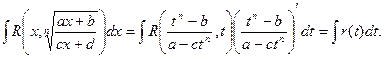
Пример. 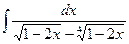
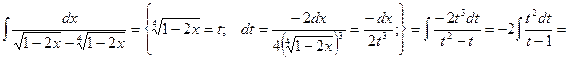
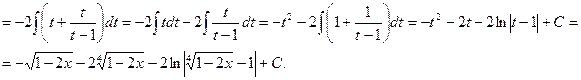
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Пример. 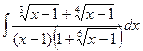
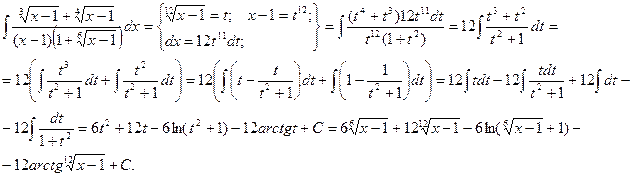
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|