Хелпикс

Главная

Контакты

Случайная статья



Тема Перпендикуляр и наклонная.

Стр 1 из 2Следующая ⇒


Тема Перпендикуляр и наклонная.

Справочный материал

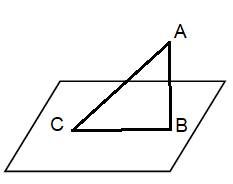Даны плоскость 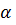и не лежащая на ней точка А.

АВ – перпендикуляр, В – основание перпендикуляра;

АС – наклонная, С – основание наклонной;

СВ – проекция наклонной;

АВ - расстоянием от точки А до плоскости .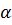

 

Определение: Перпендикуляром, опущенным из данной точки на плоскость, называется отрезок, соединяющий эту точку с точкой плоскости и лежащий на прямой, перпендикулярной данной плоскости.  

Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина   перпендикуляра, опущенного из этой точки на плоскость.

Определение: Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий точку с точкой плоскости, не являющийся перпендикуляром к плоскости.

Конец отрезка, лежащий в плоскости, называется основанием наклонной.

Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.

Теорема о трёх перпендикулярах.

Теорема 3 Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.