Хелпикс

Главная

Контакты

Случайная статья



МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

⇐ ПредыдущаяСтр 2 из 2


МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Державний університет телекомунікацій

Індивідуальне завдання №1

з вищої математики

Модуль 1 «Лінійна алгебра»

для студентів напряму підготовки

«Безпека інформаційних і комунікаційних систем»

(І семестр)

Київ 2015


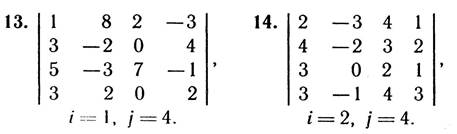
1. Для даного визначника Δ знайти мінори і алгебраїчні доповнення елементів a23, ai2, a3j. Обчислити визначник Δ:

а) розклавши його за елементами і -го рядка;

б) розклавши його за елементами j -го стовпця;

в) отримавши попередньо нулі у і -му рядку;

г) отримавши попередньо нулі у j -му стовпці;

д) звівши його до ступінчастого вигляду.

 

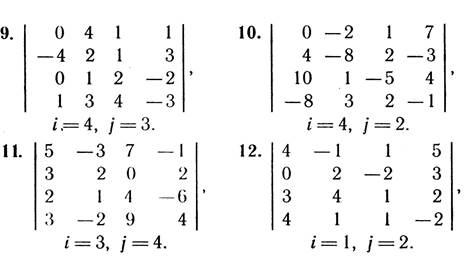
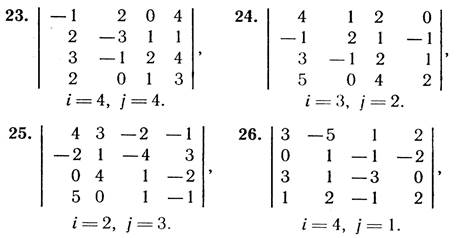
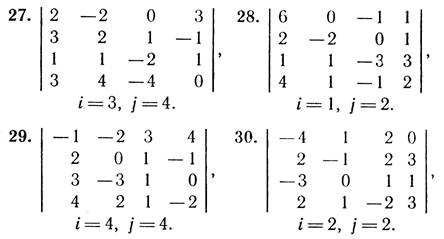
2. Дано дві матриці А і В. Обчислити:

а) добутки АВ; ВА; A2; B2;

б) матриці А-¹, В-¹ – обернені до матриць А та В, якщо це можливо.

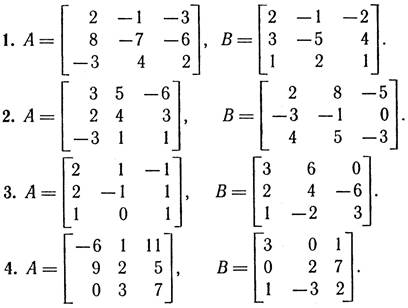
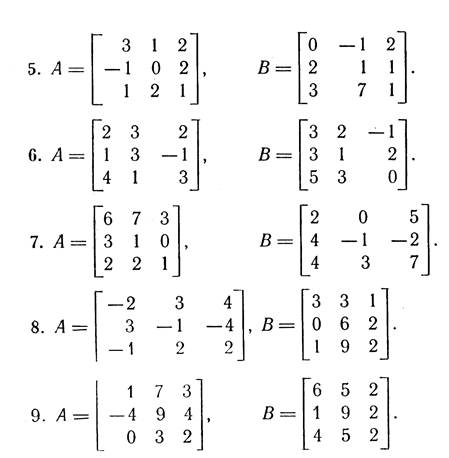
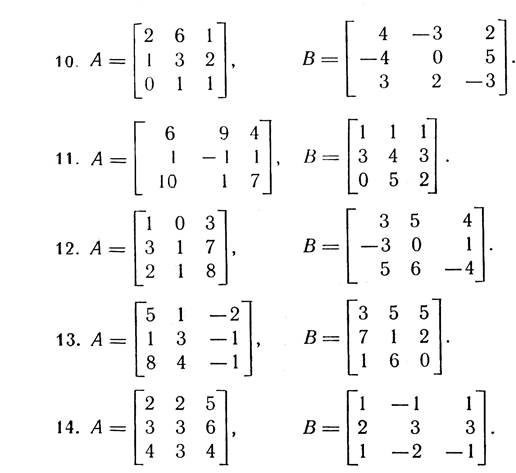
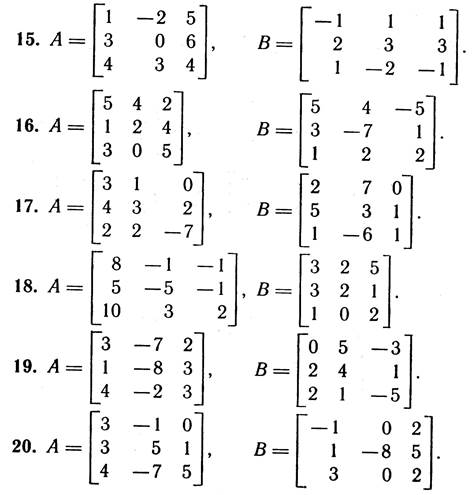
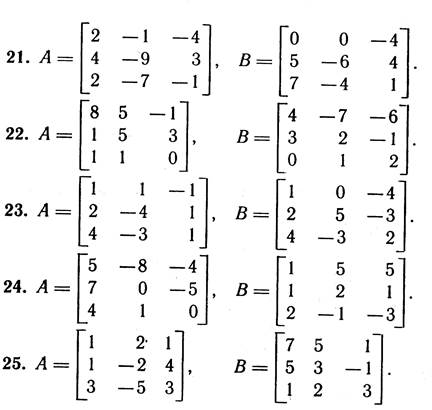
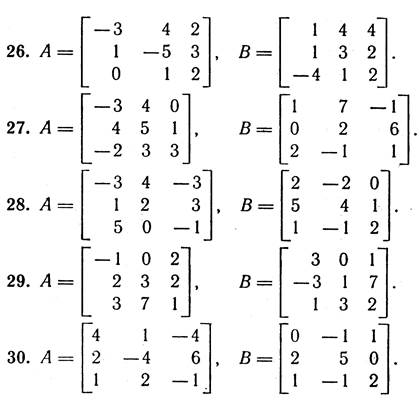
3. Перевірити СЛР на сумісність і у випадку сумісності розв’язати її:

а) за формулами Крамера;

б) матричним способом;

в) методом Гаусса.

 

 

 

 

 

 

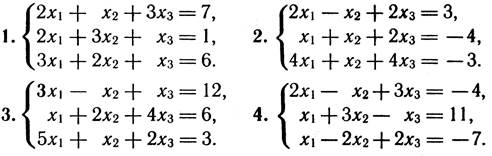
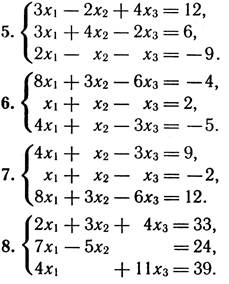
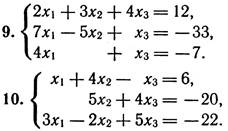
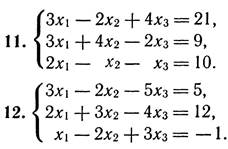
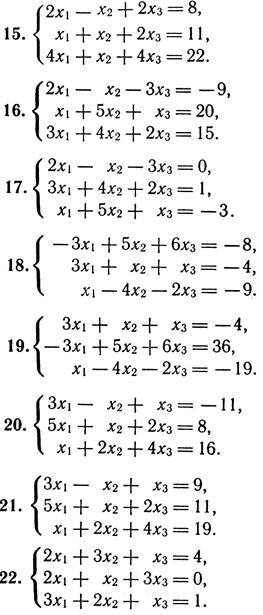
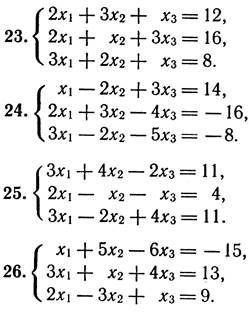
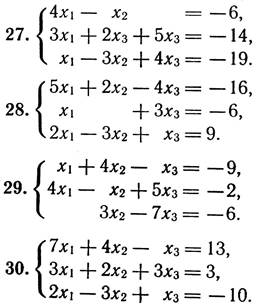
4. Перевірити СЛР на сумісність і у випадку сумісності розв’язати її:

а) за формулами Крамера;

б) матричним способом;

в) методом Гаусса.

 

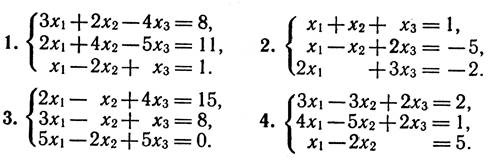
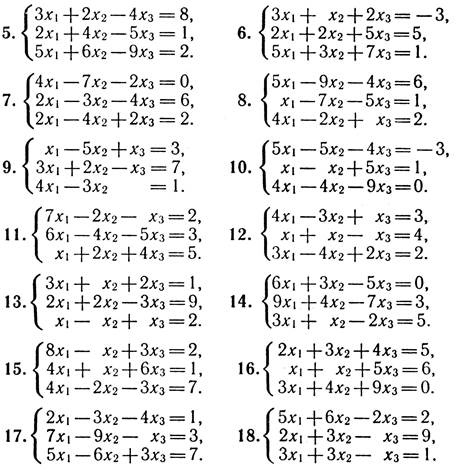
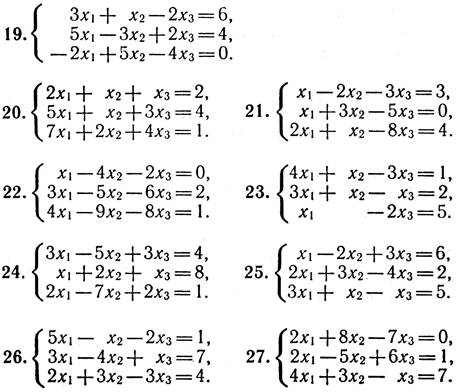
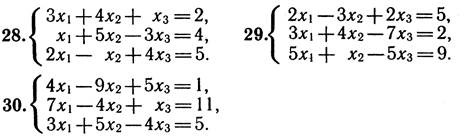
5. Розв’язати ОСЛР, вказати фундаментальну систему розв’язків та простір розв’язків ОСЛР.

 

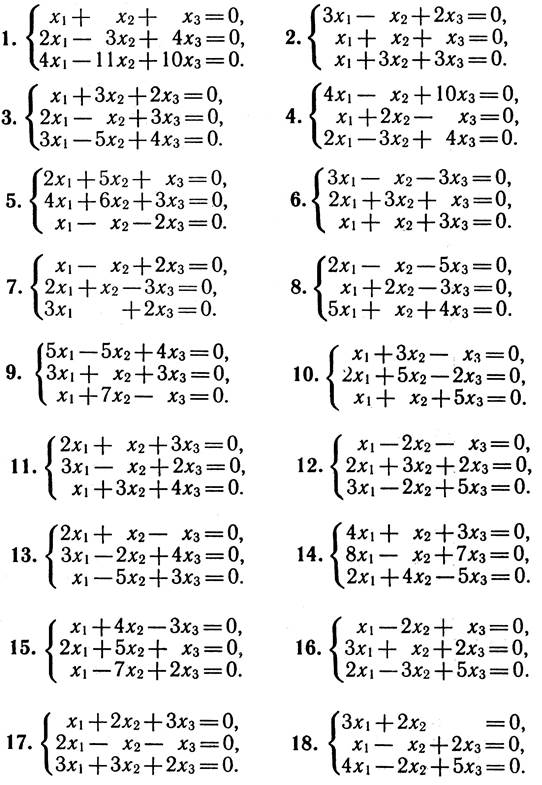
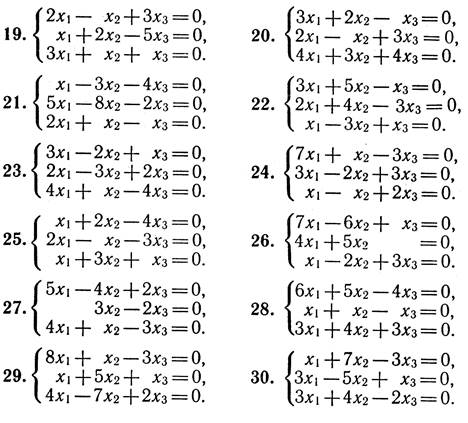
6. Розв’язати ОСЛР, вказати фундаментальну систему розв’язків та простір розв’язків ОСЛР.

 


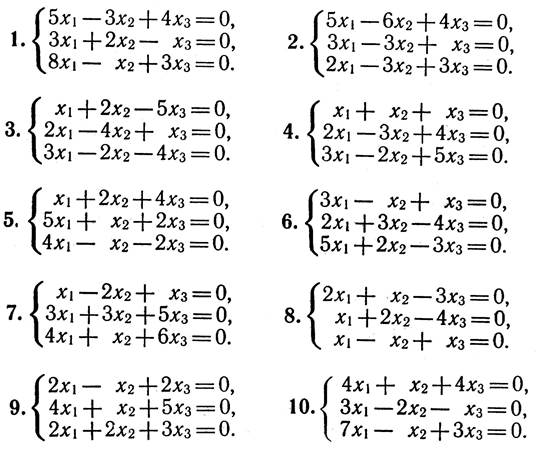
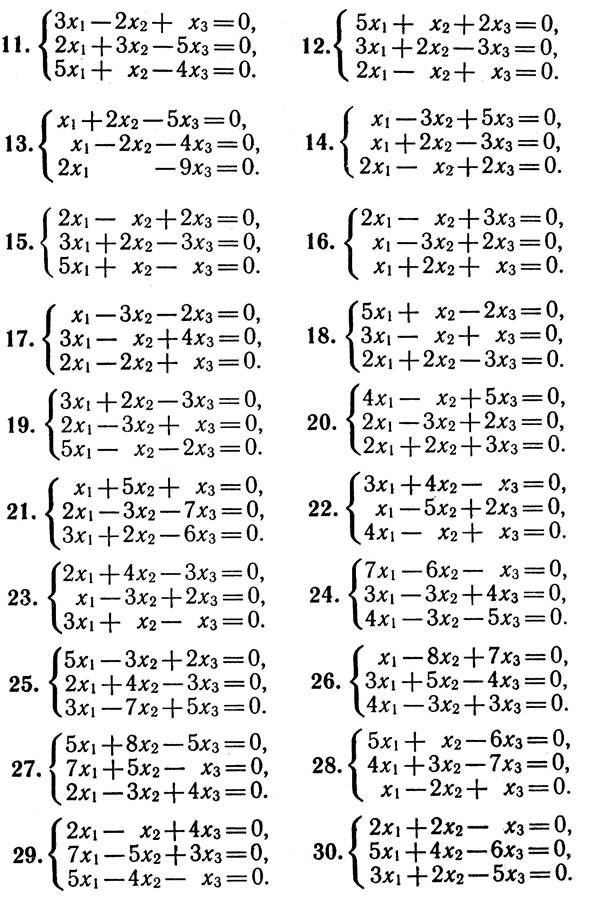
Додаток

Умови задач:

 

 

1. Для даного визначника Δ знайти мінори і алгебраїчні доповнення елементів a23, ai2, a3j. Обчислити визначник Δ:

а) розклавши його за елементами і-го рядка;

б) розклавши його за елементами j-го стовпця;

в) отримавши попередньо нулі у і-му рядку;

г) отримавши попередньо нулі у j-му стовпці;

д) звівши його до ступінчастого вигляду.

 

2. Дано дві матриці А і В. Обчислити:

а) добутки АВ; ВА; A2; B2;

б) матриці А-¹, В-¹ – обернені до матриць А та В, якщо це можливо.

 

3. Перевірити СЛР на сумісність і у випадку сумісності розв’язати її:

а) за формулами Крамера;

б) матричним способом;

в) методом Гаусса.

 

4. Перевірити СЛР на сумісність і у випадку сумісності розв’язати її:

а) за формулами Крамера;

б) матричним способом;

в) методом Гаусса.

 

5. Розв’язати ОСЛР, вказати фундаментальну систему розв’язків та простір розв’язків ОСЛР.

 

6. Розв’язати ОСЛР, вказати фундаментальну систему розв’язків та простір розв’язків ОСЛР.


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.