Раздел I. Случайные события. 1.1. Вероятность события. Основные понятия и определения.

Раздел I. Случайные события

1. 1. Вероятность события. Основные понятия и определения.

1. 1. 1. Алгебра событий

Теория вероятностей – это раздел математики, в которой изучаются закономерности случайных явлений, то есть явлений, которые при многократном их повторении протекают с некоторыми отличиями. В природе нет ни одного физического явления, в котором не присутствовали бы элементы случайности.

Достаточно часто встречаются ситуации, когда результат проводимого опыта нам предвидеть заранее невозможно. Но мы можем указать возможные результаты наших действий, кроме того, можем сказать, какой результат более, а какой менее возможен. Количественную оценку меры нашей уверенности в наступлении события и позволяет дать теория вероятностей.

Понятие события является неопределяемым, базовым понятием теории вероятностей, его нельзя свести к другим, уже известным понятиям математики. Но можно дать следующую интуитивную трактовку этого понятия. Под событием будем понимать всякий факт, который может произойти или не произойти в результате некоторого опыта (испытания). При этом опытом считаем действие, которое можно повторить неограниченное число раз. Можно сказать, что события – это возможные исходы (результаты) опыта. Например, если опыт заключается в броске игрального кубика, то некоторыми связанными с ним исходами будут: выпадение одного очка, выпадение пяти очков, выпадение четного числа очков и т. д. Если опыт заключается в том, что произведен выстрел по мишени, то исходами будут: промах стрелком, попадание стрелком.

События принято обозначать заглавными буквами .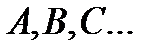

Рассмотрим пример. Пусть испытание состоит в том, что игральный кубик брошен один раз. Тогда с этим опытом можно связать достаточно большое число событий. Вот некоторые из них:

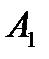- событие, состоящее в том, что выпало 1 очко,

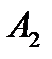- событие, состоящее в том, что выпало 2 очка,

…

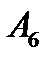- событие, состоящее в том, что выпало 6 очков,

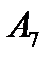- событие, состоящее в том, что выпало нечетное число очков,

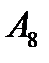- событие, состоящее в том, что выпало четное число очков,

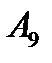- событие, состоящее в том, что выпало число очков от 1 до 6,

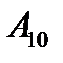- событие, состоящее в том, что выпало 10 очков,

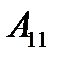- событие, состоящее в том, что выпало не более двух очков.

Заметим, что даже до проведения опыта мы абсолютно уверены в том, что событие 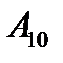не наступит. Такие события принято называть невозможными и обозначать символом Ø. Напротив, в появлении события 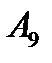мы уверены абсолютно. Такие события принято называть достоверными и обозначать . Все остальные события приведенного выше списка могут произойти, но могут и не произойти. Такие события принято называть случайными. При этом и достоверное, и невозможное события рассматриваются как разновидности случайного события.

Определение. Суммой событи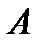й и 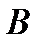называется событие 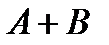, состоящее в наступлении события 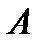или .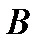

Это означает что выражению 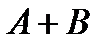соответствуют следующие ситуации: наступило 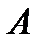, но не наступило 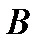; не наступило 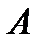и наступило 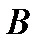; наступило 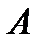и наступило 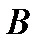. Можно сказать, что суммой событи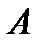й и 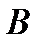является событие, состоящее в наступлении хотя бы одного из событи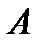й и 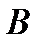. Аналогично определяется сумма большего числа событий.

Определение. Произведением событий 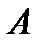и 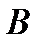называется событие 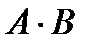, состоящее в наступлении и события 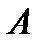, и события .

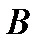Определение. Событие 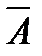, состоящее в том, что событие 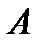не произошло, называется противоположным для .

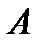Отметим, что .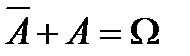

Непосредственно из определения операций над событиями получаем следующие свойства, справедливые для любых событий:

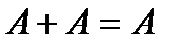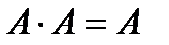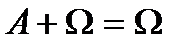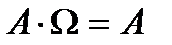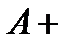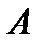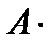, , , , Ø = , Ø 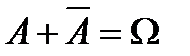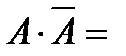=Ø, ,

Ø, , , .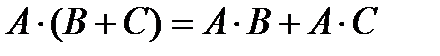

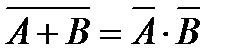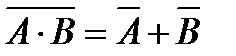Определение. Говорят, что события 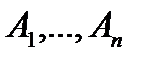образуют полную группу, если в результате опыта хотя бы одно из них обязательно произойдет, то есть .

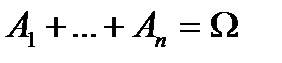Примерами событий, образующих полную группу, будут: 1) выпадение герба и выпадение решки при броске монеты, 2) промах и попадание при стрельбе по мишени, 3) хотя бы одно попадание и хотя бы один промах при двух выстрелах по мишени.

Определение. События называются несовместными, если появление одного из них в данном испытании исключает появление других в этом же испытании.

При решении задач теории случайных событий часто применяются формулы комбинаторики.

1. 1. 2. Размещения, перестановки, сочетания

Различают три основных вида комбинаций: размещения, перестановки, сочетания. В основе формул, по которым определяется число размещений, перестановок, сочетаний, лежат правила комбинаторики.

Определение. Размещениями из n элементов по m в каждом называются такие комбинации, из которых каждая содержит m различных элементов, взятых из данных n элементов, и которые отличаются друг от друга хотя бы одним элементом или порядком их расположения.

Пример. Найдите все размещения из четырех элементов по три.

Решение. Пусть множество данных элементов имеет вид: 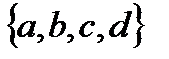. Воспользуемся методом перебора. Получаем:

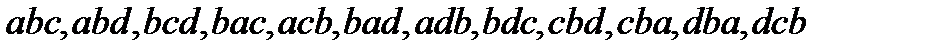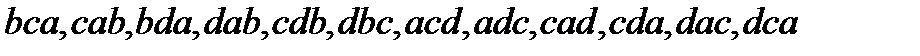Итак, всего 24 комбинации, в каждой из которых ровно три различных элемента, взятых из данных четырех элементов; любые две комбинации отличаются элементом или порядков их расположения.

Если число элементов в множестве достаточно велико, а нас интересуют не сами комбинации, а их количество, то разумнее будет воспользоваться следующей формулой.

Число размещений из n элементов по m обозначают обычно символом 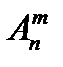и вычисляют по формуле:

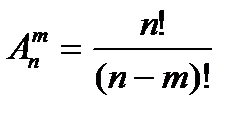Здесь 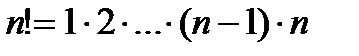- факториал натурального числа 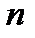. По определению полагают, что .

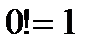Итак, возвращаясь к предыдущему примеру, получаем:

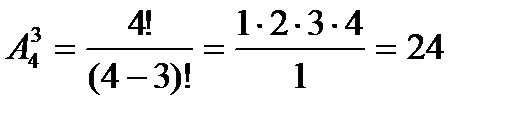Определение. Перестановками из n элементов называются такие комбинации, из которых каждая содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Пример. Найдите все перестановки из трех элементов.

Решение. Пусть множество данных элементов имеет вид: 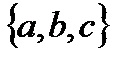. Тогда перестановками будут:

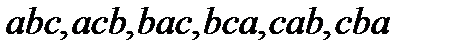Всего их получилось 6, в каждой из них по три элемента из данных трех элементов, отличаются комбинации только порядком записи элементов.

Число перестановок из n элементов обозначается символом 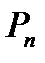и вычисляется по формуле:

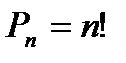
Определение. Сочетаниями из n элементов по m в каждом называются такие комбинации, из которых каждая содержит m различных элементов, взятых из данных n элементов, и которые отличаются друг от друга хотя бы одним элементом.

Пример. Найдите все сочетания из четырех элементов по три.

Решение. Пусть множество данных элементов имеет вид: 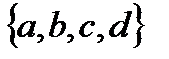. Воспользуемся методом перебора. Получаем:

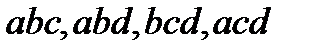Итак, всего 4 комбинации, в каждой из которых ровно три различных элемента, взятых из данных четырех элементов; любые две комбинации отличаются хотя бы одним элементом. Заметим, что с точки зрения сочетани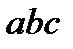й и - одна и та же комбинация.

Число сочетаний из n элементов по m обозначается символом 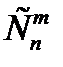и вычисляется по формуле:

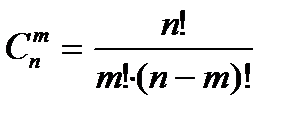1. 1. 3. Классическое определение вероятности

Существует целый класс опытов, для которых вероятности их возможных исходов (событий, связанных с опытами) нетрудно определить, опираясь непосредственно на условия опытов. Это возможно в том случае, если разные исходы опыта имеют одинаковые шансы появления. Тогда можно применить прием непосредственного подсчета вероятности события. Исход испытания назовем благоприятствующим наступлению события 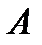, если появление этого исхода влечет за собой наступление события А. Например, пусть опыт заключается в броске игрального кубика, событие А – выпадение четного числа очков. Тогда благоприятствующих событию А исходов будет три – выпадение двух, четырех, шести очков.

Определение. Вероятностью 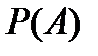случайного события А называется отношение числа m исходов некоторого испытания, благоприятствующих наступлению А, к общему числу n равновозможных несовместных исходов, возможных в данном испытании:

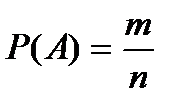Классическая формула для вычисления вероятности события А может применяться только в тех случаях, когда опыт обладает симметрией возможных исходов.

Пример. В ящике находится 6 красных, 3 синих и 5 черных пуговиц. Наугад взята одна пуговица. Найдите вероятность того, что взятая пуговица:

1) окажется красного цвета,

2) не является черной.

Решение. 1. Пусть A – событие, состоящее в том, что наугад взятая пуговица оказалась красного цвета. Найдем 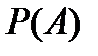- вероятность события А. По условию задачи n=6+3+5=14 – общее число исходов испытания (может быть взята любая из пуговиц), m=6 – число исходов, благоприятных для события А (так как красных пуговиц по условию 6). Тогда по классическому определению вероятности получаем:

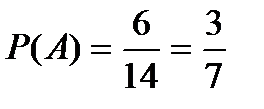2. Пусть В – событие, состоящее в том, что наугад взятая пуговица не черного цвета. Найдем 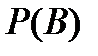- вероятность события В. Опять n=6+3+5=14 – общее число исходов испытания (может быть взята любая из пуговиц), m=6+3=9 – число исходов, благоприятных для события В (это число пуговиц, не являющихся черными, то есть красных или синих). Тогда по классическому определению вероятности получаем

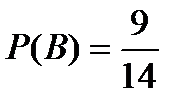1. 1. 4. Задача о выборке

Рассмотрим модельную ситуацию так называемой «задачи о выборке».

Пример. В ящике имеется 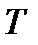деталей, из которых 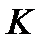бракованных. Требуется определить вероятность того, что из взятых наугад 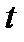деталей бракованными окажутся ровно .

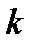Решение. Пусть 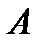- событие, состоящее в том, что из взятых наугад 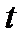деталей бракованными окажутся ровно .

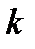Общее число способов, которыми можно изъять из коробки, в которой 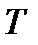деталей, ровно 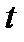деталей любого качества, равно числу сочетаний из 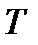элементов по 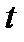, то есть 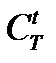. Таким образом, 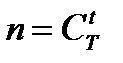- общее число исходов данного испытания (изъятия из 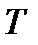деталей ровно 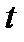деталей).

Теперь определяем число исходов, благоприятствующих наступлению события 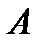. Число способов, которыми модно взять 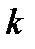бракованных деталей из имеющихся 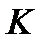бракованных, равно 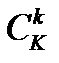. Число способов, которыми можно взять 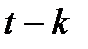качественных деталей из имеющихся 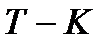качественных деталей, равно 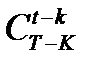. Тогда по комбинаторному правилу умножения получаем 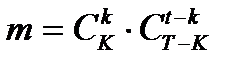- число исходов, благоприятствующих наступлению события .

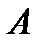Далее, по классическому определению вероятности 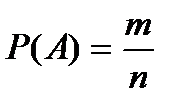, получаем

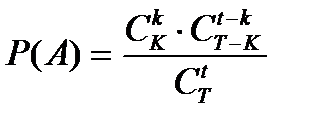Пример. Студент выучил 20 вопросов из 25 к экзамену. Какова вероятность того, что он ответит на все три вопроса преподавателя?

Решение. Пусть событие 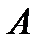состоит в том, что студент ответит на три вопроса преподавателя. Найдем число благоприятных исходов. Общее число способов, которыми можно выбрать 3 вопроса из 25 вопросов к экзамену находим по формуле 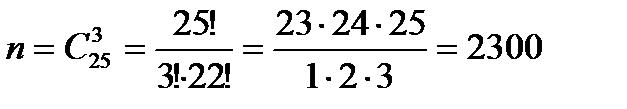. Теперь найдем количество благоприятных исходов. Количество способов, которыми можно выбрать 3 вопроса из 20 вопросов и 0 вопросов из 5, вычисляем по формуле:

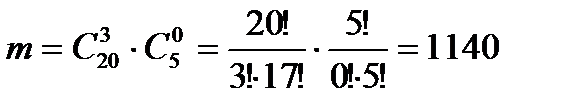По классическому определению вероятности имеем: .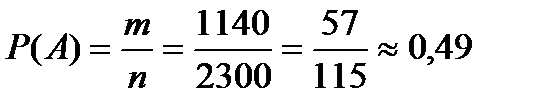

Заметим, что в задаче о выборке совершенно не является существенным то, о каких объектах идет речь. Важно то, что они подразделяются на объекты разных категорий (качественные или бракованные детали, черные или другого цвета шары, мужчины и женщины, синие или зеленые пуговицы и т. д. ), а требуется определить вероятность выбора набора объектов, из которых одна часть – одной категории, остальные – другой категории.