Тема. Понятие производной

Тема. Понятие производной

Преде́ л фу́ нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

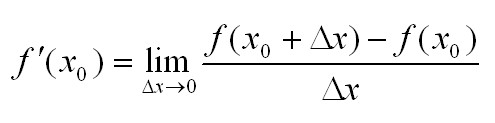
Иначе это можно записать так:

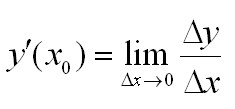
Дифференцирование функции - операция определения производной рассматриваемой функции.

Функция f(x) является непрерывной в точке x0, если предел слева равен пределу справа и совпадает со значением функции в точке x0.

Выполнить задания:

№ 1 (1)

№ 3(1, 3)

Учебник: Колягин Ю. М. Алгебра и начала анализа. 11 кл., стр. 3-8, 11-13