Определитель квадратной матрицы 2 и 3 порядков.

Определитель квадратной матрицы 2 и 3 порядков.

Пусть 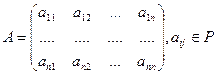- квадратная матрица с действительными или комплексными элементами.

Определение. Определителем квадратной матрицы называется алгебраическая сумма 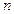! слагаемых, каждое из которых представляет собой произведение 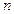элементов матрицы, взятых точно по одному из строки и каждого столбца, знак слагаемого определяется особым правилом.

Примеры: 1) ,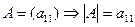

2) ,

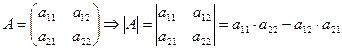3) .

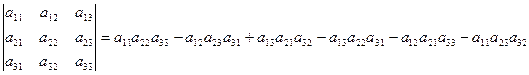Вычисление определителя матрицы третьего порядка удобно производить по следующей схеме (по правилу треугольника):

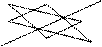
|A| = .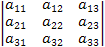

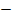
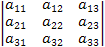Пример.

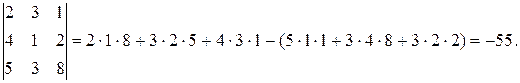
С увеличением порядка определителя очень быстро растёт количество слагаемых, в него входящих, поэтому для вычисления определителей более высокого порядка надо изучить их свойства.

Свойства определителя квадратной матрицы

1. При транспонировании матрицы определитель квадратной матрицы не меняется.

2. Определитель матрицы, имеющей две одинаковые или пропорциональные строки (или столбца) равен нулю.

3. Если все элементы какой-либо строки (столбца) умножить на число λ, то определитель матрицы умножится на λ.

4. Определитель диагональной матрицы равен произведению элементов по главной диагонали.

5. Определитель треугольной матрицы равен произведению элементов по главной диагонали.

6. При перестановке любых двух строк (столбцов) определитель матрицы меняет знак.

7. Если какому-либо столбцу (строке) матрицы А прибавить линейную комбинацию других столбцов (строк), то определитель матрицы не изменится.

8. Если i–ая строка квадратной матрицы А порядка n есть сумма m слагаемых, то определитель матрицы А равен сумме определителей m матриц А⁽¹⁾, …, А⁽^m⁾, причем элементами i-ой строки матрицы А⁽¹⁾ являются первые слагаемые i-ой строки матрицы А, элементами i-ой строки матрицы А⁽²⁾- вторые слагаемые i-ой строки матрицы А, …, элементами i-ой строки матрицы А⁽^m⁾ – m-ые слагаемые i-ой строки матрицы А, а остальные строки этих матриц совпадают со строками матрицы А. Аналогичное свойство справедливо и для столбцов матрицы А.

9. Если какая – либо строка (столбец) матрицы А является линейной комбинацией других строк (столбцов), то |А| = 0.