Теорема Больцано-Коши.

Важное значение в приложениях играет теорема о структуре области значений функции, непрерывной на промежутке.

Т. 16. 2

Область значений функции 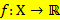, , 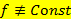непрерывной на промежутке Х, является промежуток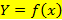

Доказательство:

Пусть , .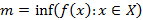

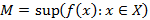Так как 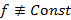, m< M. Выберем любое вещественное число С, принадлежащее интервалу 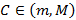и докажем, что для некоторого 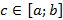выполняется равенство: 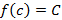. Тем самым будет доказано, что множество 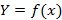значений функции является промежутком.

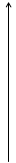По свойству нижней и верхней граней множества Y:

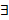такие значения A=f(a); B=f(b), что

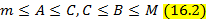
Для определенности будем считать, что A < B. Далее посредством равенства:

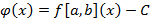
Определим непрерывную функцию на отрезке [a, b]: 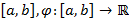. Очевидно, что 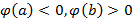. Покажем, что в некоторой точке интервала [a, b] функция f обращается в нуль. Рассмотрим множество Z:

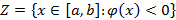. Пусть c=sup(Z). Заметим, что c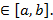

Действительно, поскольку в некоторой окрестности 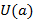функция 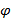сохраняет знак числа 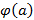, то есть отрицательна, то будет выполняться такое включение.

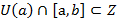, a < c

Поскольку в некоторой окрестности U(b) функция 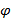сохраняет знак числа 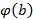, то есть положительна, то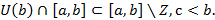

Докажем, что 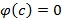. Предполагая противное будем иметь 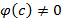, но тогда в некоторой окрестности 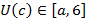функция 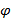либо строго отрицательна, либо строго положительна, смотря по знаку числа 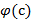. В любом случае это противоречит тому, что 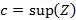. Так как:

1) 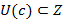, число не может быть верхней границей множества Z.

2) 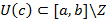, число с не может быть наименьшей верхней границей числа Z.

Получается противоречие, доказывающее, что 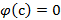. То есть 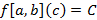. Следовательно, 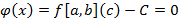. На отрезке [a, b] совпадает с функцией f.

Теорема доказана.