
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ. МЕТАЛЛОВ И ПОЛУПРОВОДНИКОВ ОТ ТЕМПЕРАТУРЫ. Саратов 2011
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ
МЕТАЛЛОВ И ПОЛУПРОВОДНИКОВ ОТ ТЕМПЕРАТУРЫ
Методические указания к выполнению
лабораторных работ по физике для студентов
всех специальностей всех форм обучения
Одобрено и рекомендовано к печати
научно-методическим семинаром
кафедры «Общая физика» СГТУ
Саратов 2011
Составители – Вахлюева Валентина Ивановна.
Минаев Евгений Николаевич
Боженькин Василий Михайлович.
Беляев Илья Викторович
Рецензент – д. т. н., профессор кафедры ОФ Сысоев Виктор Владимирович
© Саратовский государственный
технический университет 2011 г.
ОСНОВНЫЕ ПОНЯТИЯ
Электропроводность веществ – это величина, обратная их электрическому сопротивлению, характеризует условия, в которых протекает ток. В СИ электропроводность измеряется в сименсах. Электропроводностью в 1 См обладает вещество, сопротивление которого равно 1 Ом. Важной характеристикой веществ является также их удельная электропроводность g - величина, обратная удельному сопротивлению r.
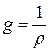 .
.
В СИ электропроводность измеряется См/м. Металлы хорошо проводят ток и имеют удельную электропроводность порядка 107 – 105 См/м. Удельная электропроводность диэлектриков составляет 10-8 – 10-16 См/м. Полупроводники обладают удельной электропроводностью порядка 10-8 – 105 См/м. У большинства веществ электропроводность сильно зависит от температуры.
Запишем закон Ома в дифференциальной форме
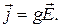 (1)
(1)
где 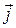 - плотность тока,
- плотность тока, 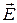 - напряженность электрического поля, под действием которого перемещаются носители тока. Напомним, что носителями тока в веществе могут являться электроны, дырки, ионы.
- напряженность электрического поля, под действием которого перемещаются носители тока. Напомним, что носителями тока в веществе могут являться электроны, дырки, ионы.
Если в веществе одновременно присутствуют носители обоих знаков (например, положительные и отрицательные ионы в электролитах, электроны и дырки в полупроводниках), то положительные носители движутся по направлению вектора напряженности 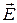 , и электропроводность складывается из электропроводности положительных носителей g+ и электропроводности отрицательных носителей g-.
, и электропроводность складывается из электропроводности положительных носителей g+ и электропроводности отрицательных носителей g-.
Тогда
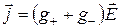 (2)
(2)
Плотность тока равна общему заряду, который пройдет за 1 секунду через единицу площади поперечного сечения проводника. Эти заряды заключены в объёме цилиндра, площадь основания которого равна единице, а высота – средней скорости 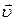 упорядоченного движения зарядов под действием электрического поля. Если в единице объёма находится n зарядов, численное значение плотности тока выразится формулой
упорядоченного движения зарядов под действием электрического поля. Если в единице объёма находится n зарядов, численное значение плотности тока выразится формулой
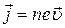 , (3)
, (3)
где  е – заряд электрона или дырки.
е – заряд электрона или дырки.
Сравнивая (1) и (3), получим
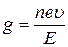 (4)
(4)
Величина 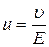 носит название подвижности носителей тока, показывает, какую скорость приобретут заряды под действием единичной напряженности
носит название подвижности носителей тока, показывает, какую скорость приобретут заряды под действием единичной напряженности 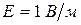 . Таким образом, подвижность носителей тока – величина, равная отношению средней скорости направленного движения носителей тока, вызванного электрическим полем, к напряженности поля.
. Таким образом, подвижность носителей тока – величина, равная отношению средней скорости направленного движения носителей тока, вызванного электрическим полем, к напряженности поля.
Перепишем уравнение (4)
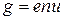 (5)
(5)
Следовательно, удельная электропроводность веществ зависит от концентрации носителей (количества носителей в единице объёма вещества) n, заряда носителя е и его подвижности u. Если в веществе одновременно существуют два типа носителей, то
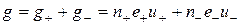 (6)
(6)
ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
В металлах, как правило, носителями тока являются электроны. Электропроводность металлов
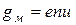 .
.
Концентрация электронов в металлах очень велика – порядка 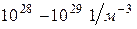 и почти не зависит от температуры. Из зонной теории проводимости известно, что в металлах валентная зона и зона проводимости перекрываются.
и почти не зависит от температуры. Из зонной теории проводимости известно, что в металлах валентная зона и зона проводимости перекрываются.
Чтобы электроны начали упорядоченно двигаться под действием электрического поля, они должны изменить свою энергию. С квантовой точки зрения, электрон может принять небольшую энергию лишь в том случае, если существуют близкие энергетические уровни, не занятые другими электронами. Под действием приложенного внешнего электрического поля электроны переходят на свободные энергетические уровни зоны проводимости при любой температуре, и в проводнике возникнет ток.
Средняя скорость упорядоченного движения электронов в веществе чрезвычайно мала (10-3 м/с) по сравнению со средней скоростью их теплового движения при обычных температурах, что объясняется частыми столкновениями электронов c ионами кристаллической решетки. Модель свободных электронов – грубое приближение к реальной картине твёрдого тела. Положительно заряженные ионы – узлы кристаллической решетки – создают внутри металла электрическое поле, влияющее на движение электронов проводимости. Узлы решетки расположены в пространстве в строгом порядке. Поэтому, создаваемое ими электрическое поле – периодическая функция координат, которая приводит к существенному изменению энергетических состояний электронов в твёрдом теле по сравнению с их состоянием в изолированных атомах. (см. «Основы зонной теории полупроводников», 2011 г. )
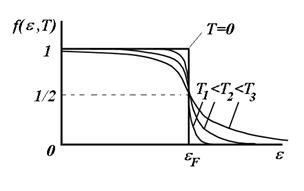
Распределение электронов по различным квантовым состояниям в условиях теплового равновесия подчиняется статистике Ферми-Дирака, которая учитывает принцип Паули. Согласно этой статистики вероятность того, что квантовое состояние с энергией Е занято при температуре Т электроном (с любой ориентацией спина) равно:
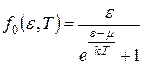 (7)
(7)
где m - энергия Ферми, максимальная энергия которой могут обладать электроны при данной температуре или химический потенциал, отнесенный к отдельной частице; 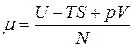 , где U – внутренняя энергия системы, S – энтропия, V – объём системы, р – давление, N – число частиц в системе. Химический потенциал – энергия Ферми – выражает работу, которая затрачивается при данных условиях на увеличение числа частиц системы на единицу.
, где U – внутренняя энергия системы, S – энтропия, V – объём системы, р – давление, N – число частиц в системе. Химический потенциал – энергия Ферми – выражает работу, которая затрачивается при данных условиях на увеличение числа частиц системы на единицу.
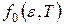 – функция распределения Ферми – равна 1, если
– функция распределения Ферми – равна 1, если 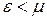 ; ½, если
; ½, если 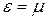 ; 0, если
; 0, если 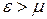 .
.
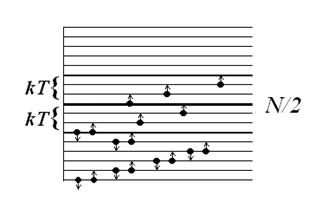 Все энергетические уровни, расположенные выше уровня Ферми при абсолютном нуле свободны, то есть имеем резкую границу между занятыми и свободными квантовыми состояниями. При повышении температуры граница расплывается. Электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни, вследствие чего меняется характер распределения их по состояниям. Пока
Все энергетические уровни, расположенные выше уровня Ферми при абсолютном нуле свободны, то есть имеем резкую границу между занятыми и свободными квантовыми состояниями. При повышении температуры граница расплывается. Электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни, вследствие чего меняется характер распределения их по состояниям. Пока 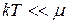 тепловому возбуждению могут подвергаться электроны лишь узкой полосы порядка
тепловому возбуждению могут подвергаться электроны лишь узкой полосы порядка 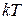 , непосредственно расположенной около уровня Ферми. В результате теплового возбуждения часть электронов, имеющая энергию, несколько меньшую m, переходит на уровни с энергией несколько большей m, и устанавливается новое их распределение по скоростям. В интервале энергий от 0 до m располагается N/2 энергетических уровней, где N – число свободных электронов в киломоле металла. Упрощая задачу, можно считать, что эти уровни отстоят друг от друга на одинаковом энергетическом расстоянии, а именно, на расстоянии
, непосредственно расположенной около уровня Ферми. В результате теплового возбуждения часть электронов, имеющая энергию, несколько меньшую m, переходит на уровни с энергией несколько большей m, и устанавливается новое их распределение по скоростям. В интервале энергий от 0 до m располагается N/2 энергетических уровней, где N – число свободных электронов в киломоле металла. Упрощая задачу, можно считать, что эти уровни отстоят друг от друга на одинаковом энергетическом расстоянии, а именно, на расстоянии 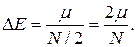 Термодинамическому возбуждению подвергаются электроны полосы
Термодинамическому возбуждению подвергаются электроны полосы 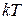 , расположенной ниже уровня Ферми. В этой полосе размещается
, расположенной ниже уровня Ферми. В этой полосе размещается 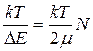 или
или 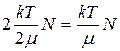 электронов. Полагая, что за уровень Ферми переходит не более половины этих электронов, получим приближенное соотношение для
электронов. Полагая, что за уровень Ферми переходит не более половины этих электронов, получим приближенное соотношение для 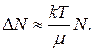
 При комнатной температуре
При комнатной температуре 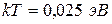 ,
, 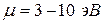 . Поэтому
. Поэтому 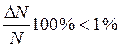 . То есть во всем диапазоне температур, в котором электронный газ в металле является вырожденным, (одной и той же энергией обладают разные квантовые состояния) его распределение мало отличается от распределения при абсолютном нуле. С повышением температуры m уменьшается. Но для металлов это уменьшение незначительно.
. То есть во всем диапазоне температур, в котором электронный газ в металле является вырожденным, (одной и той же энергией обладают разные квантовые состояния) его распределение мало отличается от распределения при абсолютном нуле. С повышением температуры m уменьшается. Но для металлов это уменьшение незначительно.
При соударении с узлами кристаллической решетки электроны, согласно классическим представлениям, полностью теряют скорость упорядоченного движения, которую они приобретают под действием внешнего электрического поля за время t свободного пробега. В процессе свободного пробега электроны движутся равноускоренно. В квантовой теории движение электронов сквозь решетку металла рассматривается как распространение де-бройлевских электронных волн, которые рассеиваются на ионах кристаллической решетки. Роль средней длины свободного пробега электрона в квантовой теории играет средняя длина пробега 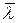 электронной волны, то есть среднее расстояние, которое волна может пройти без рассеяния на узлах кристаллической решетки. Для распространения электронных волн узлы решетки не являются жесткой преградой: электронные волны могут «обтекать» узлы и распространяться без рассеяния на значительные расстояния, то есть длина свободного пробега может составлять сотни периодов решётки. А это означает, что вероятность обнаружить электрон, прошедший в решетке сотни междуузельных расстояний, отлична от нуля. То есть электрон может свободно проходить в кристалле большие расстояния.
электронной волны, то есть среднее расстояние, которое волна может пройти без рассеяния на узлах кристаллической решетки. Для распространения электронных волн узлы решетки не являются жесткой преградой: электронные волны могут «обтекать» узлы и распространяться без рассеяния на значительные расстояния, то есть длина свободного пробега может составлять сотни периодов решётки. А это означает, что вероятность обнаружить электрон, прошедший в решетке сотни междуузельных расстояний, отлична от нуля. То есть электрон может свободно проходить в кристалле большие расстояния.
Совершенно правильная, идеальная кристаллическая решетка, в узлах которой находятся неподвижные ионы, не рассеивает электронные волны. В такой решётке отсутствуют центры рассеяния – неоднородности, искажения правильности решётки, превосходящие по размеру длину де-бройлевских волн.
Поток свободных электронов должен проходить сквозь такую решетку беспрепятственно. Подобная решетка не представляла бы никакого сопротивления для движения электронов. Электрическое сопротивление металла было бы равно нулю, если бы ионы решетки металла были бы неподвижны. Но при любой температуре частицы твердого тела в узлах решетки совершают колебания. Хаотические тепловые колебания частиц в узлах кристаллической решетки создают в ней флуктуации плотности. За счет тепловых колебаний расстояния между частицами в решетке, а следовательно и плотность вещества, могут быть неодинаковыми в соседних малых объёмах внутри металла. Ионы кристаллической решетки в результате тепловых колебаний то сближаются, то расходятся, образуя то сгущения положительных зарядов, то их разряжение, что приводит к сильным местным искажениям электрического поля. Встречая такие неоднородности поля, электроны резко изменяют направление своего движения. В этом и заключается механизм их взаимодействия с кристаллической решеткой, в процессе которого они передают решетке часть своей энергии (например, добавочную энергию, приобретенную ими под действием электрического поля) или, наоборот, получают от нее дополнительную энергию. С повышением температуры интенсивность колебаний ионов возрастает, средняя длина свободного пробега электронов уменьшается 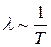 , а удельное сопротивление металлов увеличивается
, а удельное сопротивление металлов увеличивается 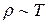 . При очень низких температурах
. При очень низких температурах 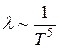 . Поэтому, в согласии с опытами, удельное сопротивление чистых металлов при сверхнизких температурах
. Поэтому, в согласии с опытами, удельное сопротивление чистых металлов при сверхнизких температурах 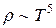 , а так как
, а так как 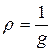 , то удельная электропроводность
, то удельная электропроводность 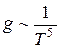 . Как показывают опыты
. Как показывают опыты 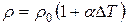 , где a - температурный коэффициент сопротивления, характеризует зависимость сопротивления вещества от температуры. Он численно равен относительному изменению сопротивления проводника при нагревании его на 1 К. Для всех металлических проводников
, где a - температурный коэффициент сопротивления, характеризует зависимость сопротивления вещества от температуры. Он численно равен относительному изменению сопротивления проводника при нагревании его на 1 К. Для всех металлических проводников 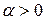 и незначительно меняется с изменением температуры. r0 – удельное сопротивление при
и незначительно меняется с изменением температуры. r0 – удельное сопротивление при 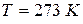 , или, что то же самое,
, или, что то же самое, 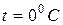 .
.
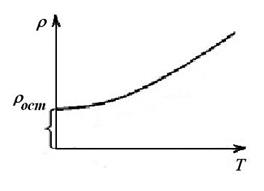 Величина
Величина 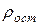 . в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле r = 0.
. в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле r = 0.
| Вещество | Температурный коэффициент сопротивления a, К-1 |
| Алюминий | 3, 8× 10-3 |
| Железо | 6, 2× 10-3 |
| Медь | 4, 8× 10-3 |
| Ртуть (жидкость) | 9× 10-4 |
| Константан (40% Ni, 60% Cu) | 2× 10-5 |
| Нихром (20% Cr, 75% Ni, 5% Fe) | 1× 10-4 |
| Фехраль (13% Cr, 4% Al, 1% Si, 0, 7% Mn, остальное Fe) | 2× 10-4 |
| Хромаль (25% Cr, 5% Al, 70% Fe) | 4× 10-5 |
Таким образом, при повышении температуры удельная электропроводность металлов уменьшается. Теоретические выводы квантовой теории металлов приводят к выводу, что 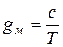 , где с – постоянная, зависящая от рода металла.
, где с – постоянная, зависящая от рода металла.
График зависимости 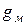 от
от 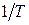 представляет собой прямую, проходящую через начало координат, угол наклона которой зависит от рода металла, так как
представляет собой прямую, проходящую через начало координат, угол наклона которой зависит от рода металла, так как 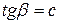 .
.
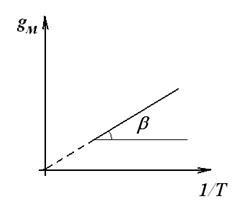 В области температур, близких к абсолютному нулю, а также при очень высоких температурах формула
В области температур, близких к абсолютному нулю, а также при очень высоких температурах формула 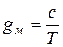 неприменима. Однако в большом интервале температур (для многих металлов от минус 100-1500С до плюс 200-3000С) линейная зависимость электропроводности металлов gм от
неприменима. Однако в большом интервале температур (для многих металлов от минус 100-1500С до плюс 200-3000С) линейная зависимость электропроводности металлов gм от 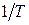 выполняется с достаточно высокой точностью.
выполняется с достаточно высокой точностью.
ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
В полупроводниках носителями тока могут быть как электроны, так и дырки (см. «Основы зонной теории полупроводников», 2011 г. ).
В полупроводнике, обладающем собственной проводимостью, концентрация электронов, перешедших в зону проводимости, равна концентрации дырок, образовавшейся в валентной зоне, поэтому для удельной электропроводности такого полупроводника справедливо выражение
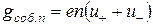 , (8)
, (8)
где 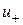 и
и 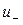 - подвижности дырок и электронов соответственно.
- подвижности дырок и электронов соответственно.
В полупроводниках, подвижность электронов и дырок различна (подвижность электронов выше, чем подвижность дырок) и зависит от температуры. В таблице приведены подвижности электронов и дырок в различных веществах.
| Вещество | Подвижность (м2 с-1 в-1 ) | |
| электроны | дырки | |
| Алмаз | 0, 18 | 0, 12 |
| Кремний | 0, 16 | 0, 04 |
| Германий | 0, 38 | 0, 18 |
| Сернистый свинец | 0, 06 | 0, 02 |
| Медь | 0, 0035 | - |
При повышении температуры подвижность как электронов, так и дырок уменьшается за счет увеличения интенсивности тепловых колебаний кристаллической решетки, препятствующих направленному движению носителей.
В то же время концентрация электронов в зоне проводимости и дырок в валентной зоне с повышением температуры резко возрастает.
При температурах, близких к абсолютному нулю, полупроводник является изолятором, так как валентная зона целиком заполнена электронами, а зона проводимости лишена электронов. При повышении температуры увеличивается средняя кинетическая энергия электронов 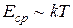 и при
и при 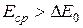 (
( 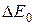 - ширина запрещенной зоны) электроны переходят из валентной зоны в зону проводимости. Число таких электронов в единицу времени будет тем больше, чем выше средняя энергия теплового движения электронов, то есть чем выше температура.
- ширина запрещенной зоны) электроны переходят из валентной зоны в зону проводимости. Число таких электронов в единицу времени будет тем больше, чем выше средняя энергия теплового движения электронов, то есть чем выше температура.
Рассчитаем температуру, при которой средняя энергия электронов достаточна для перехода их из валентной зоны в зону проводимости для германия 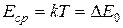 . Для германия
. Для германия 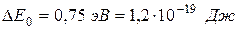 , постоянная Больцмана, тогда
, постоянная Больцмана, тогда 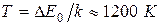 .
.
Таким образом, в германии собственная проводимость в полной мере наступает при температуре 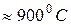 .
.
Однако следует учесть, что 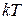 – это средняя энергия электронов. При данной температуре некоторая часть электронов имеет энергию, большую, чем
– это средняя энергия электронов. При данной температуре некоторая часть электронов имеет энергию, большую, чем 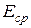 . Поэтому практически собственная проводимость в германии возникает уже при температуре 300 – 4000 С.
. Поэтому практически собственная проводимость в германии возникает уже при температуре 300 – 4000 С.
Возрастание концентрации носителей в полупроводниках при повышении температуры происходит более резко, чем уменьшение подвижности, поэтому удельная электропроводность полупроводников растет с ростом температуры. Для полупроводника, обладающего собственной проводимостью, зависимость удельной электропроводности от температуры выражается следующей формулой
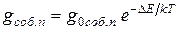 (9)
(9)
где 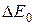 – ширина запрещенной зоны в полупроводнике.
– ширина запрещенной зоны в полупроводнике.
Для того, чтобы выяснить физический смысл величины 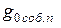 , положим в формуле (9)
, положим в формуле (9) 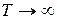 . Тогда
. Тогда 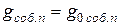 . Следовательно,
. Следовательно, 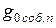 – это удельная электропроводность полупроводника, обладающего собственной проводимостью, при
– это удельная электропроводность полупроводника, обладающего собственной проводимостью, при 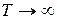 . Ясно, что
. Ясно, что 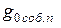 от температуры почти не зависит.
от температуры почти не зависит.
При графическом изображении зависимости удельной электропроводности полупроводника от температуры обычно пользуются полулогарифмическими координатами и строят зависимость 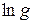 от
от 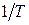 .
.
Прологарифмируем уравнение (9)
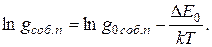 (10)
(10)
График зависимости 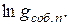 от
от 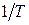 представляет собой прямую, тангенс угла наклона которой пропорционален ширине запрещенной зоны полупроводника
представляет собой прямую, тангенс угла наклона которой пропорционален ширине запрещенной зоны полупроводника 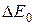 :
:
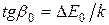 .
.
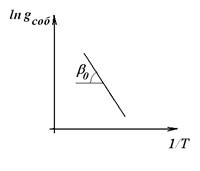
В полупроводниках, обладающих примесной проводимостью, проводимость начинается при более низкой температуре, чем в полупроводниках с собственной проводимостью. Это объясняется тем, что локальные энергетические уровни (донорные или акцепторные) расположены вблизи зоны проводимости или валентной зоны (см. «Основы зонной теории полупроводников», 2011г. ). При этом для перевода электронов с донорных уровней в зону проводимости или из валентной зоны на акцепторный уровень нужна гораздо меньшая энергия, чем для переброски электрона из валентной зоны в зону проводимости в случае собственной проводимости
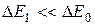 ,
,
где 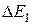 – энергия активации примеси.
– энергия активации примеси.
Рассчитаем температуру, при которой в германии n – типа происходит переход электронов с донорных уровней в зону проводимости. Для такого перехода средняя энергия электронов на донорном уровне 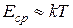 должна быть больше энергии активации
должна быть больше энергии активации 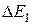 донорного уровня
донорного уровня 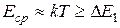 ,
, 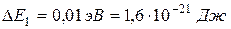 ,
, 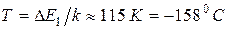 .
.
На самом деле примесная проводимость в германии начинается при минус 100 – 1600 С.
С повышением температуры удельная электропроводность полупроводников, содержащих примеси, возрастает так же, как электропроводность чистых полупроводников, по экспоненциальному закону:
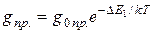 , (11)
, (11)
где 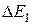 – энергия активации локального уровня,
– энергия активации локального уровня, 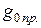 – постоянная, зависящая от рода полупроводника и слабо зависящая от температуры.
– постоянная, зависящая от рода полупроводника и слабо зависящая от температуры.
Такой характер зависимости 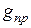 от Т сохраняется до тех пор, пока все электроны донорных уровней не будут принимать участие в проводимости n – полупроводника или все вакантные места акцепторных уровней не будут заполнены электронами в р – полупроводнике. При дальнейшем повышении температуры удельная электропроводность перестает повышаться и остаётся постоянной (или даже несколько уменьшается) до тех пор, пока не начнется собственная проводимость полупроводника. Тогда удельная электропроводность вновь начнет возрастать в соответствии с равенством (9).
от Т сохраняется до тех пор, пока все электроны донорных уровней не будут принимать участие в проводимости n – полупроводника или все вакантные места акцепторных уровней не будут заполнены электронами в р – полупроводнике. При дальнейшем повышении температуры удельная электропроводность перестает повышаться и остаётся постоянной (или даже несколько уменьшается) до тех пор, пока не начнется собственная проводимость полупроводника. Тогда удельная электропроводность вновь начнет возрастать в соответствии с равенством (9).
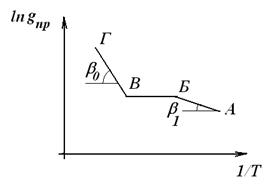 Теоретический график зависимости удельной электропроводности примесного полупроводника от температуры показан на рисунке.
Теоретический график зависимости удельной электропроводности примесного полупроводника от температуры показан на рисунке.
Кривая имеет три хорошо выраженных участка АБ, БВ и ВГ. Участок АБ соответствует низким температурам и выражает зависимость примесной электропроводности от температуры (формула 11). На этом участке 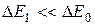 и рост электропроводности происходит в основном за счет роста концентрации примесных носителей тока в зоне проводимости или в валентной зоне. Наклон прямой АБ к оси абсцисс определяет энергию активации примеси
и рост электропроводности происходит в основном за счет роста концентрации примесных носителей тока в зоне проводимости или в валентной зоне. Наклон прямой АБ к оси абсцисс определяет энергию активации примеси 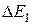
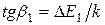 (12)
(12)
Количество примесных носителей увеличивается с ростом температуры до тех пор, пока примеси не истощатся (точка Б). Дальнейшее повышение температуры не приводит к увеличению электропроводности. Участок БВ соответствует области истощения примесей. В точке В температура достигает такой величины, что становятся возможными переходы электронов непосредственно из валентной зоны в зону проводимости.
На участке ВГ полупроводник имеет собственную проводимость, быстро растущую с ростом температуры в соответствии с формулой (9).
Угол наклона прямой ВГ к оси абсцисс пропорционален ширине запрещенной зоны полупроводника
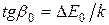 .
.
ПРОИЗВОДСТВО ИЗМЕРЕНИЙ
Цель работы состоит в установлении характера зависимости сопротивления металлов и полупроводников от температуры.
Для этого необходимо:
1. Снять зависимость сопротивления металла от температуры.
2. Построить график зависимости R металла от Т.
3. Определить температурный коэффициент сопротивления 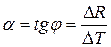 .
.
4. Снять зависимость сопротивления полупроводника от температуры.
5. Построить график зависимость 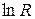 полупроводника от
полупроводника от 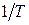 .
.
6. Определить по графику ширину запрещенной зоны примесного полупроводника или энергию активации примесей в полупроводнике.
Металлический образец представляет собой тонкий медный провод, намотанный на катушку. В качестве полупроводникового образца используется термосопротивление. Образцы помещены в сосуды с маслом, которое нагревается.
Зависимость сопротивления металлов от температуры, определяется рассеиванием электронов на колебаниях кристаллической решетки и подчиняется закону:
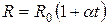 (13)
(13)
где R0 – сопротивление проводника при 00 C, a - температурный коэффициент сопротивления (ТКС), t – температура (в градусах по шкале Цельсия), которая определяется по градуировочному графику, представленному на стенде.
Графическая зависимость сопротивления от температуры есть прямая линия с положительным угловым коэффициентом:
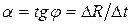 .
.
Сопротивление идеально чистых полупроводников, определяемое процессом генерации носителей заряда при нагревании, падает с ростом температуры по закону:
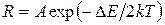 , (14)
, (14)
где R – сопротивление проводника при температуре Т, А – величина, слабо зависящая от температуры (этой зависимостью мы в дальнейшем пренебрегаем), 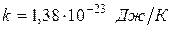 – постоянная Больцмана. Аналогично меняется и сопротивление примесных полупроводников.
– постоянная Больцмана. Аналогично меняется и сопротивление примесных полупроводников.
Если прологарифмировать выражение (14), то получим 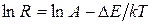 .
.
Это представление удобнее, так как график зависимости 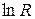 от
от 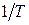 – есть прямая линия с отрицательным угловым коэффициентом -
– есть прямая линия с отрицательным угловым коэффициентом - 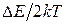 , и тогда ширина запрещенной зоны
, и тогда ширина запрещенной зоны 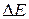 может быть определена графически по коэффициенту наклона прямой
может быть определена графически по коэффициенту наклона прямой 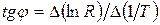 :
: 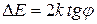 , где
, где 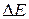 – энергия активации примеси. Энергию активации собственного полупроводника, то есть ширину запрещенной зоны чистого полупроводника на данной установке невозможно.
– энергия активации примеси. Энергию активации собственного полупроводника, то есть ширину запрещенной зоны чистого полупроводника на данной установке невозможно.
Данные эксперимента и расчетов занести в таблицу:
| Металл | Полупроводник | |||||
| R | U | T | R | U | T | DE |
| … | …. | |||||
Для проведения измерения необходимо:
1. Соединить проводниками клеммы Rx реохордного моста с клеммами Rx на панели лабораторного стенда, содержащего исследуемые экземпляры металла и полупроводника.
2. На стенде:
а) включить питание переменным током;
б) переключатель диапазонов поставить в положение «установка нуля»;
в) гальванометр – в положение «установка нуля» и проверить положение стрелки на нуле (в центре шкалы).
3. Переключатель диапазонов установить в положение ´ 1000 для металлов или в положение ´ 10 (´ 100) – для полупроводников. Переключатель на гальвано-метре установить в положение «ГРУБО».
4. Тумблером «МЕТАЛЛ – ПОЛУПРОВОДНИК», расположенном на стенде, выбрать одно из двух положений, а другим тумблером «СЕТЬ» включить нагреватель образца.
5. Для измерения сопротивления образца вращать ручку изменения сопротивлений плеч реохорда (большая шкала) и добиться установки стрелки гальванометра на ноль. В этом положении записать показания шкалы, то есть величину сопротивления (не забудьте о значениях множителей переключателя диапазонов! ) и, одновременно, показания милливольтметра на стенде (переводить в температуру по графику). По мере нагревания образца такие измерения проводятся несколько раз (9 – 10).
6. Выключить тумблер «СЕТЬ». Тумблер «МЕТАЛЛ – ПОЛУПРОВОДНИК» переключить на второй образец и провести измерения (пункт 5) в режиме остывания образца.
7. По результатам измерений построить график зависимости сопротивления образцов от температуры.
8. Используя данные эксперимента для металла определить температурный коэффициент сопротивления 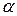 .
.
9. Используя данные эксперимента для полупроводника, построить график зависимости 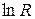 от
от 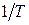 и вычислить
и вычислить 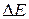 - энергию активации примеси полупроводника.
- энергию активации примеси полупроводника.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что называется удельной электропроводностью вещества и в каких интервалах изменяется удельная электропроводность различных групп веществ?
2. Как выглядит закон Ома в дифференциальной форме для металлов и полупроводников?
3. Что является носителями тока в металлах, полупроводниках, электролитах?
4. Что называется подвижностью носителей тока? Одинакова ли она для различных носителей? Как она зависит от температуры?
5. От каких величин зависит удельная электропроводность металлов и полупроводников?
6. Объясните механизм собственной и примесной проводимости полупроводников.
7. Как влияет повышение температуры на концентрацию электронов в зоне проводимости металла?
8. Объясните механизм возникновения сопротивления у металлов.
9. Распределение Ферми – Дирака. Энергия Ферми.
10. Как квантовая теория объясняет возникновение сопротивления у металлов?
11. Что такое температура вырождения?
12. Температурный коэффициент сопротивления.
13. Как влияет повышение температуры на концентрацию носителей тока в полупроводниках?
14. Объясните зависимость электропроводности полупроводника и сопротивления от температуры.
15. Энергия активации локальных уровней. График зависимости 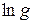 от
от 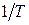 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|