Теорема синусов. Доказательство теоремы синусов

Теорема синусов

Теорема синусов устанавливает зависимость между величиной углов треугольника и противолежащих ему сторон.

Формулировка теоремы синусов:
Стороны треугольника пропорциональны синусам противолежащих углов

или,

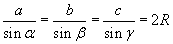
где
R - радиус описанной вокруг треугольника окружности
a, b, c - стороны треугольника
α, β, γ - величины противолежащих этим сторонам углов

Доказательство теоремы синусов

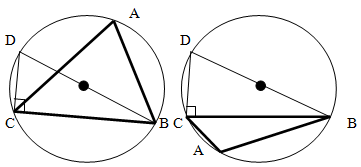
Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.
Для доказательства всей теоремы, поскольку размеры треугольника выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R. Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.

Проведем диаметр BD для описанной окружности. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность).

Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π - CAB (в противном случае).

Обратимся к свойствам тригонометрических функций. Поскольку sin( π − α ) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.

Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника.

2R = BC / sin A
2R = BC / ( BC / DB )
2R = DB

А, поскольку, DB строился как диаметр окружности, то равенство выполняется.
Повторив то же рассуждение для двух других сторон треугольника, получаем:

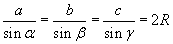
Теорема синусов доказана.