Теоремы об отрезках пересекающихся хорд и о квадрате касательной

Теоремы об отрезках пересекающихся хорд и о квадрате касательной

Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство. Пусть E — точка пересечения хорд AB и CD (рис. 110). Докажем, что AE * BE = CE * DE.

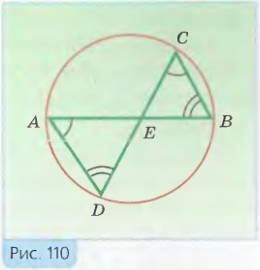
Рассмотрим треугольники ADE и CBE. Их углы A и C равны, так как они вписанные и опираются на одну и ту же дугу BD. По аналогичной причине ∠ D = ∠ B. Поэтому треугольники ADE и CBE подобны (по второму признаку подобия треугольников). Таким образом, DE/BE = AE/CE, или

AE * BE = CE * DE.

Теорема доказана.

Теорема. Если через точку M проведены касательная MK, где K – точка касания, и секущая, пересекающая окружность в точках A и B, то MK² = MA * MB.

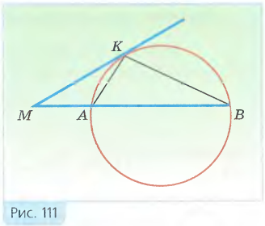Доказательство. Проведем отрезки AK и BK (рис. 111). Треугольники AKM и KBM подобны по второму признаку подобия треугольников: угол M у них общий, а углы AKM и B равны, так как каждый из них измеряется половиной дуги AK (угол AKM — это угол между касательной и хордой, а угол B – вписанный). Поэтому MK/MB = MA/MK, или MK² = MA * MB. Теорема доказана.