
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Триангуляция.
Триангуляцией называют построенные на местности фигуры из треугольников, в которых измерены все углы и одна или, для целей контроля, две из сторон.
Вершины треугольников закрепляют подземными центрами и обозначают наземными знаками – сигналами и пирамидами. В таких треугольниках по формулам тригонометрии легко находятся недостающие величины, что позволяет вычислять координаты вершин треугольников.
Триангуляционные сети используются в качестве основы для топографических съёмок, для производства разбивочных работ, а также для наблюдений за осадками и деформациями зданий и сооружений. В зависимости от назначения геодезической сети, размеров и формы объекта изысканий или строительства форма триангуляционных построений, размеры сторон и точность измерений в триангуляционных сетях могут значительно различаться.
Некоторые типовые схемы простейших триангуляционных построений приведены на рис. 2. 2. На рисунках измеренные стороны, называемые базисами, обозначены буквой b. В качестве исходных базисов и пунктов могут быть использованы стороны сетей более высокого класса (рис. 2. 2, б, в).

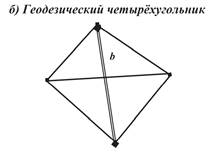
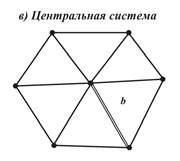
Рис. 2. 2. Некоторые типовые схемы триангуляционных построений
Отличительной особенностью триангуляционных построений является минимальный объём линейных измерений, что являлось весьма весомым аргументом в пользу триангуляции во времена, когда электронные способы измерения расстояний ещё не были известны.
В таблице 2. 2 приведены некоторые требования к развитию опорной инженерно-геодезической сети способом триангуляции для построений 4 класса 1 и 2 разрядов.
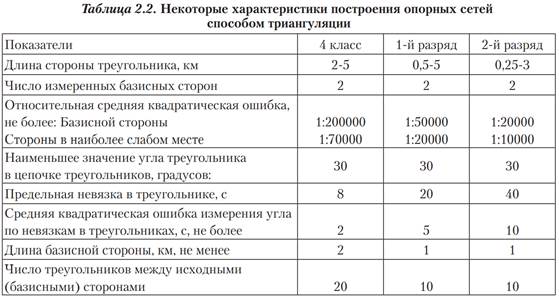
Специальные инженерно-геодезические сети, построенные способом триангуляции (например, тоннельная триангуляция, гидротехническая триангуляция или мостовая триангуляция) имеют другие технические показатели, причём более жёсткие.
В соответствии с действующими нормативными документами основными показателями класса триангуляции являются средние квадратические ошибки измеренных углов mβ , средние относительные ошибки наиболее слабых сторон m a /a и ошибки исходных сторон (базисов) m b /b.
Для разбивочных сетей характерной особенностью является соблюдение заданной ошибки во взаимном положении соседних пунктов или пунктов, образующих опорную сторону для разбивочных работ. Такая специфика разбивочных сетей обусловлена тем, что с её пунктов производится разбивка точек, принадлежащих одному сооружению. Требования к взаимному положению точек некоторых сооружений могут быть достаточно жёсткими.
Триангуляционная сеть 4 класса проектируется на карте, руководствуясь при этом нормативными требованиями СП. Сеть должна быть локальной, хотя отдельные её пункты могут быть совмещены с имеющимися на карте пунктами государственной сети, считая их пунктами более высокого класса.
Проектируя сеть на карте, следует руководствоваться тем положением, что наблюдения углов в сети будут выполняться со штатива на пирамиды высотой 6-8 м. Условия прохождения визирного луча между пунктами могут быть определены по профилям местности.
Выбор схемы или формы сети остаётся за проектировщиком в соответствии с условиями местности. Для территорий городов, населённых пунктов и строительных площадок могут оказаться целесообразными центральные системы или системы из треугольников, покрывающих весь участок.
В триангуляционной сети обязательно должно быть не менее двух исходных (базисных) сторон. В случае, если на участке имеется твёрдая сторона (между существующими пунктами), в проекте должно быть предусмотрено измерение ещё одной базисной стороны. Выполнение этих требований обеспечивает контроль масштаба сети. Для наглядности проект сети (в уменьшенном масштабе) отдельным рисунком изображается на отдельном листе бумаги (например, рис. 2. 3).
Для предварительной оценки проекта типичных схем построения сети можно пользоваться приближёнными формулами. Оценка в данном случае сводится к определению средней квадратической ошибки взаимного положения пунктов слабой стороны запроектированной сети. Слабой считается наиболее удалённая от обоих базисов сторона. При равенстве числа треугольников до разных сторон наиболее слабой будет сторона с наименьшей длиной.
На рис. 2. 3 приведен ряд триангуляции (цепочка треугольников), опирающийся на две исходные базисные стороны b1 и b2. Стороны S1, S2, …, общие для двух соседних треугольников, называют связующими, а противолежащие им углы A, B, – связующими углами.
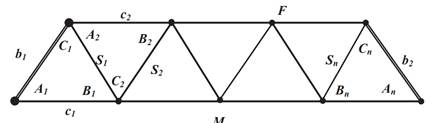
Рис. 2. 3. Ряд триангуляции
Стороны S используются в последовательных вычислениях координат вершин треугольников, и проходящую по ним линию называют ходовой. Так сторона S1 определится из соотношения
S1= 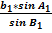 (2. 1)
(2. 1)
Для стороны S2 будем иметь
S2= 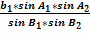 (2. 2)
(2. 2)
В такой последовательности, решая треугольники, находят все стороны S ходовой линии.
Стороны с1, c2 называют промежуточными, а противолежащие им углы С1, С2 – промежуточными углами.
Средняя квадратическая ошибка связующей стороны цепочки, опирающейся на две исходные базисные стороны, может быть определена по известным приближённым формулам. Эти формулы основаны на сложении весов оцениваемой стороны. Веса определяются через среднюю квадратическую ошибку оцениваемой стороны. Ошибку вычисляют дважды: от начальной и конечной базисных сторон.
Если среднюю квадратическую ошибку стороны МF = S, полученную от базисной стороны b 1, обозначить через m S1, а от базисной стороны b2 – через m S2, то соответствующие веса стороны S будут равны
p1 = μ 2/ , p2 = p1 = μ 2/.
Вес среднего значения длины стороны определится по формуле:
p = p1+p2= μ 2 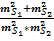 , (2. 3)
, (2. 3)
а средняя квадратическая ошибка определяемой стороны S будет:
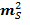 = μ 2/p=
= μ 2/p= 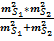 (2. 4)
(2. 4)
Средние квадратические ошибки ms определяются по формуле.
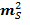 =
= 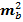 +
+  *S2*
*S2* 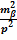 Σ (ctg2Ai+ctg Bi+ ctg2Ai*ctg Bi) (2. 5)
Σ (ctg2Ai+ctg Bi+ ctg2Ai*ctg Bi) (2. 5)
Эта формула записана в предположении, что mAi = mBi = mβ и стороны в треугольниках приблизительно равны, т. е. S1 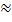 S2
S2 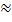
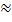 S
S 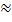 b1
b1 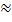 b2. Для сети в виде центральной системы или геодезического четырёхугольника коэффициент перед S2 будет равен 0, 5.
b2. Для сети в виде центральной системы или геодезического четырёхугольника коэффициент перед S2 будет равен 0, 5.
Величина Σ (ctg2Ai+ctg Bi+ ctg2Ai*ctg Bi) не зависит от точности измерений, а только от значений углов Ai и Вi, т. е. от формы треугольников; её называют ошибкой геометрической связи или обратным весом треугольников и обозначают Σ R. Величины R табулированы и выбираются по связующим углам А и В. Углы для этих целей измеряются транспортиром по схеме на карте. Также по карте определяют длины сторон. Если вычисления производятся для измерений по направлениям, то
mβ = mн* 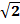 .
.
Ошибка исходной стороны mb практически всегда значительно меньше ошибок измерений развиваемой сети, хотя бы в два раза:
т. е. mb/b 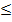 d ms/2S.
d ms/2S.
Поэтому, опустив mb в формуле 2. 5, можно найти ms, задавшись mβ , и наоборот.
Формулу 2. 4 из аналогичных рассуждений можно записать и для дирекционных углов связующих сторон треугольников:
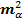 =
=  , (2. 6)
, (2. 6)
где 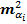 = 2/3
= 2/3 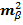 *k, а k – число треугольников от базисной стороны до данной, оцениваемой.
*k, а k – число треугольников от базисной стороны до данной, оцениваемой.
Поперечная ошибка конечного пункта стороны S определится по формуле
mq =( 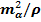 )*L,
)*L,
где L = S1 + S2 + ··· + S 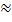 k ·Sср – диагональ звена.
k ·Sср – диагональ звена.
Ошибку взаимного положения пунктов М и F находят из выражения
m2=m2(S)+m2(α ),
где первый член формулы отражает ошибку в длине стороны, а второй – ошибку её дирекционного угла, или, иначе,
m2=m2(S)+(mα /ρ )2L2,
Сказанное поясняет рис. 2. 4.

Рис. 2. 4. Ошибки угловых и линейных измерений
Исходя из принципа равных влияний ошибок угловых и линейных измерений, можно записать mS=(mα /ρ )L,
PĮ /ȡ )·L, что позволит вычислить ошибку взаимного положения пунктов М и F по вычисленному значению mS.
Итак, m2=2m2s. Найденное значение m сравнивают с допустимым. При удовлетворительном результате по принятому значению mβ определяют класс сети и точность измерения базиса. В противном случае берут за основу другое значение mβ , иначе говоря, назначают более высокий класс сети и расчёты повторяют.
Для оценки проекта сети на компьютере, имеющем соответствующую программу уравнивания (оценки) параметрическим способом, необходимо определить по карте или на схеме в масштабе в условной системе приближённые координаты всех пунктов.
Как правило, во все программы для оценки проекта параметрическим способом необходимо ввести следующие данные:
• номер исходных точек и их координаты;
• среднюю квадратическую ошибку измеренного угла;
• приближённые координаты определяемых пунктов.
Обычно при оценке проектов принимают один из пунктов в качестве исходного, а координаты определяются по километровой сетке карты.
В результате оценки будут получены обратные веса функции определения координат всех пунктов и их средние квадратические ошибки по осям координат mx и my. Средняя квадратическая ошибка М планового положения пункта может быть приближённо подсчитана по формуле
M= 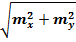 (2. 7)
(2. 7)
Максимальное значение этой ошибки, соответствующее наиболее слабо определяемому пункту, сравнивается с допустимой величиной 2, 5 см. Далее делается вывод и принимается соответствующее решение. Следует иметь в виду, что во многих программах заложена и оценка функции определения взаимного положения пунктов в наиболее слабо определяемом месте сети. Эту величину так же можно сравнить с допустимой и принимать соответствующее решение.
Основными достоинствами метода триангуляции являются его оперативность и возможность использования в разнообразных физико-географических условиях. Метод позволяет непосредственно в поле осуществлять контроль измеренных величин и с высокой точностью определять взаимное положения смежных пунктов сети. Проектирование триангуляционных сетей выполняют на топографических картах 1: 10000 и 1: 25000 исходя из назначения сети, формы и площади территории, её рельефа и застроенности, наличия пунктов государственной сети и других параметров.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|