Исследование функции на монотонность

Функция у=ƒ (х) называется возрастающей в промежутке α < x< b, если

для любых х₁ и х₂, принадлежащих этому промежутку и таких, что х₁< х₂, имеет место неравенству ƒ (х₁)< ƒ (х₂).

Функция у=ƒ (х) называется убывающей в промежутке α < x< b, если для любых х₁ и х₂, принадлежащих этому промежутку и таких, что х₁< х₂, имеет место неравенству ƒ (х₁)> ƒ (х₂).

Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает – промежутками монотонности.

Возрастание и убывание функции у=ƒ (х) характеризуется знаком её производной: если в некотором промежутке ƒ '(х)> 0, то функция возрастает в этом промежутке; если же ƒ '(х)< 0, то функция убывает в этом промежутке.

Пример 1.

Найти промежутки монотонности функции

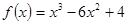
1. Найдем производную ƒ '(х):

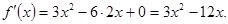
2. Приравняем производную к нулю и найдем критические точки.

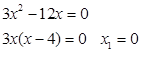или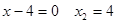

Критические точки разбивают область определения на три промежутка.

3. Найдем знак производной в каждом из промежутков, подставив любое значение из промежутка в производную. В промежутках, где ƒ '(х)> 0 – функция возрастает, а где ƒ '(х)< 0 функция убывает.

ƒ '> 0 ƒ '< 0 ƒ '> 0

функция 0 функция 4 функция х

возрастает убывает возрастает

4. Составим таблицу:

х	-∞ < x< 0	0< x< 4	4< x< ∞
ƒ '(х)	+	-	+
ƒ (х)	ä	æ	ä

Итак, в промежутках -∞ < x< 0 и 4< x< ∞ функция возрастает,

а в промежутке 0< x< 4 – убывает.

Задачи для самостоятельного решения

1. Найдите промежутки монотонности следующих функций.

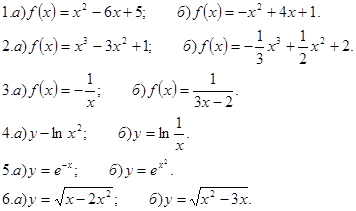
Попробуйте сделать №№ 1, 2, 3.