
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ТАБЛИЦА 1. Таблица неопределённых интегралов. ТАБЛИЦА 2. Основные свойства неопределённого интеграла. ТАБЛИЦА 3. Таблица основных дифференциалов или таблица «хвостиков». ТАБЛИЦА 4. Примеры использования свойства №4. ТАБЛИЦА 5. Вычисление площадей плоских
ТАБЛИЦА 1
Таблица неопределённых интегралов
| № | Формула | № | Формула |
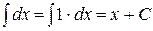
| 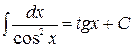
| ||
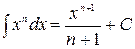 , где , где 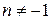
| 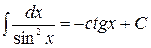
| ||
| 2* | 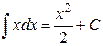
| 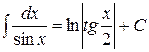
| |
| 2** | 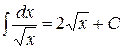
| 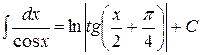
| |
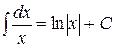
| 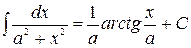
| ||
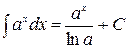
| 13* | 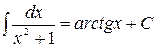
| |
| 4* | 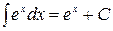
| 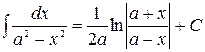
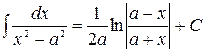
| |
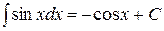
| 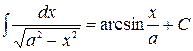
| ||
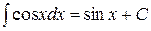
| 15* | 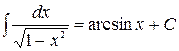
| |
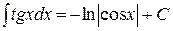
| 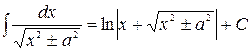
| ||
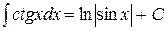
|
Замечание 1: при использовании ТАБЛИЦЫ 1 можно следующим образом заменять числа: например, 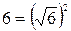 , но нельзя таким же образом заменять переменные: например,
, но нельзя таким же образом заменять переменные: например, 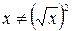
Замечание 2: Часто встречающиеся интегралы:
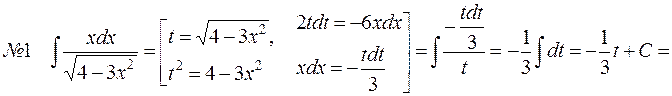
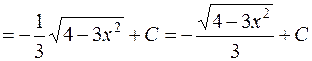
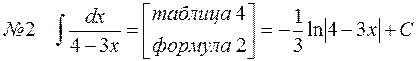
ТАБЛИЦА 2
Основные свойства неопределённого интеграла
| № | Свойство | Формула |
| Постоянный множитель выносится за знак интеграла | 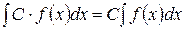 , где , где 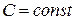
| |
| Интеграл от суммы двух функций равен сумме интегралов от этих функций | 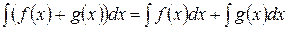
| |
| Интеграл от производной функции по dx равен самой функции | 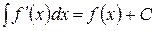 , где , где 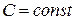 ,
т. к. ,
т. к. 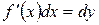 , а , а 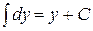
| |
Интеграл от функции 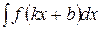
| 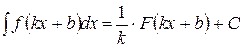 ,
где ,
где 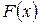 - первообразная для функции - первообразная для функции 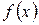 ; ; 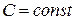
|
ТАБЛИЦА 3
Таблица основных дифференциалов или таблица «хвостиков»
| № | Формула | № | Формула |
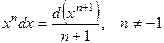
| 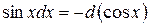
| ||
| 1* | 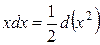
| 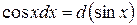
| |
| 1** | 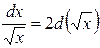
| 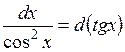
| |
| 2 | 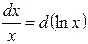
| 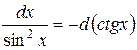
| |
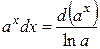
| 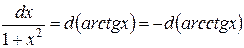
| ||
| 3* | 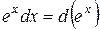
| 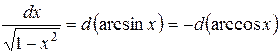
|
ТАБЛИЦА 4
Примеры использования свойства №4
| № | Формула | № | Формула |
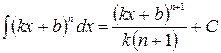
| 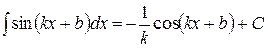
| ||
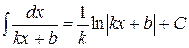
| 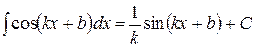
| ||
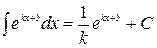
| 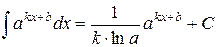
|
ТАБЛИЦА 5
Вычисление площадей плоских фигур в декартовой системе координат
| № | Описание фигуры | Рисунок | Формула |
Фигура ограничена сверху графиком 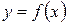 , снизу – осью Оx, сбоку прямыми , снизу – осью Оx, сбоку прямыми 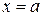 , , 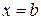
| 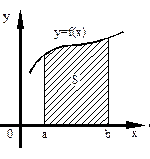
| 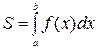
| |
Фигура ограничена сверху графиком функции 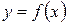 , снизу – графиком функции , снизу – графиком функции 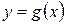 , а сбоку прямыми , а сбоку прямыми 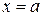 , , 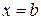
| 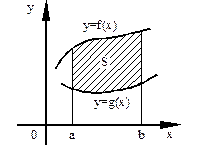
| 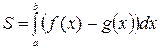
| |
Фигура ограничена сверху осью Оx, снизу – графиком функции 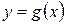 , а сбоку прямыми , а сбоку прямыми 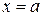 , , 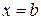
| 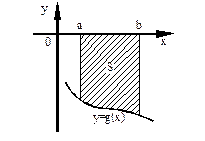
| 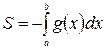
| |
| В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить ее на сумму или разность двух или более криволинейных трапеций | 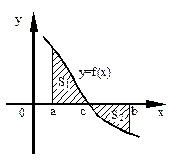
| 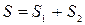 ,
где ,
где 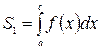 , ,
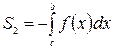 . .
| |
Фигура ограничена слева осью Oy, справа – графиком функции 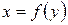 , а снизу и сверху прямыми , а снизу и сверху прямыми 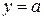 , , 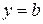 соответственно соответственно
| 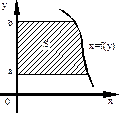
| 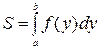
| |
Фигура ограничена слева графиком функции 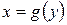 , справа – графиком функции , справа – графиком функции 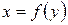 , а снизу и сверху прямыми , а снизу и сверху прямыми 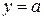 , , 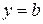 соответственно соответственно
| 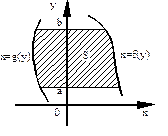
| 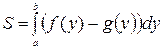
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|