Градиентный спуск. Алгоритм. Соотношение Канторовича

Градиентный спуск

Градиентный спуск — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.

Пусть целевая функция имеет вид:

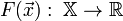И задача оптимизации задана следующим образом:

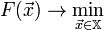
Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом :

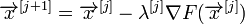
где 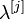выбирается

§ постоянной, в этом случае метод может расходиться;

§ дробным шагом, т. е. длина шага в процессе спуска делится на некое число;

§ наискорейшим спуском: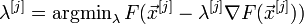

Алгоритм

1. Задают начальное приближение и точность расчёта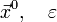

2. Рассчитывают 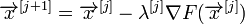, где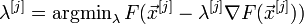

3. Проверяют условие остановки:

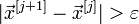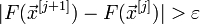§ Если , или 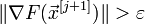(выбирают одно из условий), то 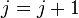и переход к шагу 2.

§ Иначе 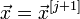и останов.

Соотношение Канторовича

Для квадратичной функции вида 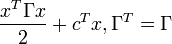метод наискорейшего градиентного поиска сходится из любой начальной точки 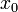со скоростью геометрической прогрессии (линейно) со знаменателем, не превосходящим значение 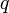. При этом справедливы следующие оценки:

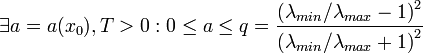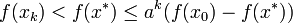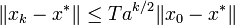где 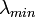и 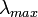- минимальное и максимальное собственные числа числа матрицы вторых производных .

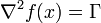Таким образом, поскольку функция близка в малом к своей квадратичной аппроксимации, скорость сходимости, в окрестности точки минимума, зависит от отношения собственных чисел. Чем больше это отношение, тем хуже сходимость метода.