
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производная функции. Правила дифференцирования. Формулы дифференцирования. Найти производную функции
Производная функции
Производной функции 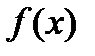 в точке
в точке  называется предел разностного отношения
называется предел разностного отношения 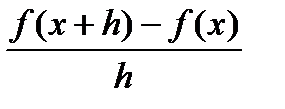 при
при 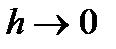 :
: 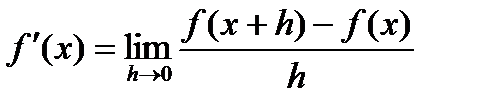
Дифференцирование – это операция вычисления производной.
Обозначения производной (штрих): 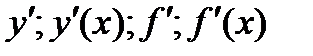
Правила дифференцирования
1. Постоянный множитель можно вынести за знак производной: 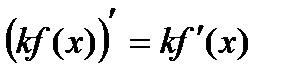
2. Производная суммы: 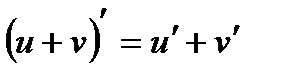
Формулы дифференцирования
1) 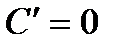 ,
, 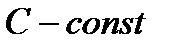
2) Степенная функция: 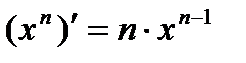 , следствия:
, следствия: 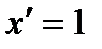 и
и 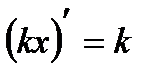
3) 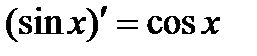 4)
4) 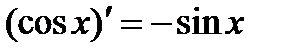
5) 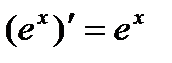 6)
6) 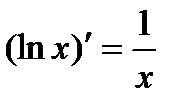
7) 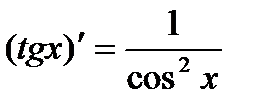 8)
8) 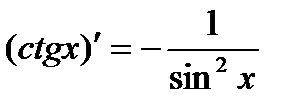
Найти производную функции
Пример 1. 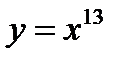 (применяем формулу 2)
(применяем формулу 2)
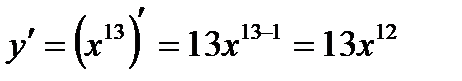
Пример 2. 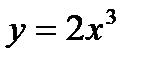 (применяем правило 1 и формулу 2)
(применяем правило 1 и формулу 2)
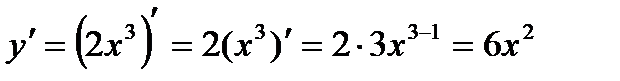
Пример 3. 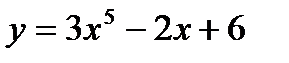 (применяем правило 1. и 2.; формулы 1), 2) и следствия)
(применяем правило 1. и 2.; формулы 1), 2) и следствия)
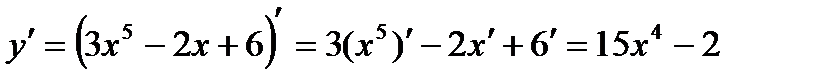
Пример 4. 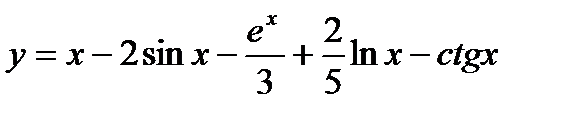 (применяем правило 1. и 2.; затем формулы)
(применяем правило 1. и 2.; затем формулы) 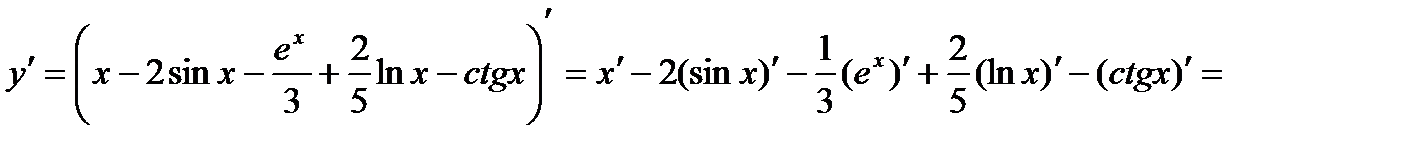
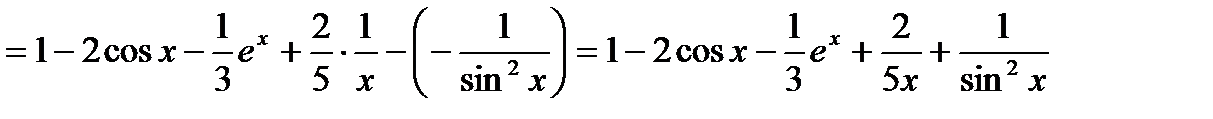
Найти производную функции в точке:
- найти производную данной функции по правилам и формулам дифференцирования;
- подставить заданное значение аргумента 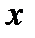 в найденную производную.
в найденную производную.
Пример 5. Найти 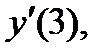 если
если 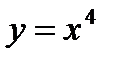
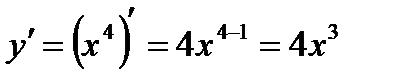
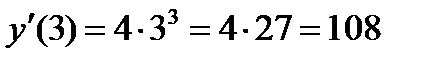
Пример 6. Найти 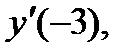 если
если 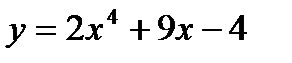
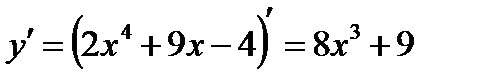
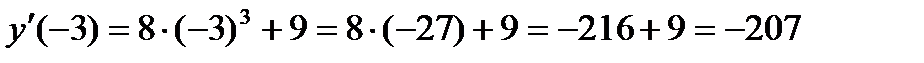
Пример 7. Найти 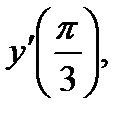 если
если 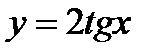
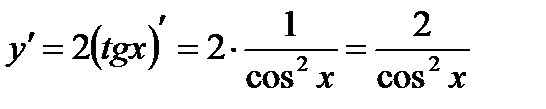
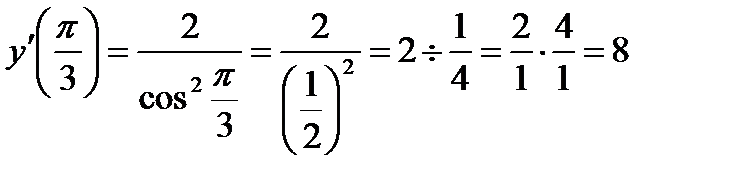
Пример 8. Найти 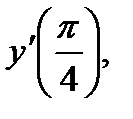 если
если 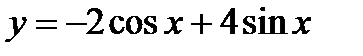
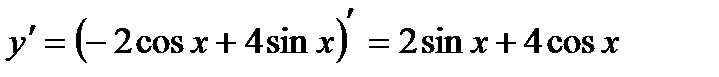
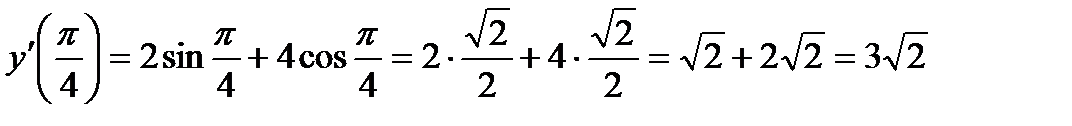
Задания для самостоятельного решения:
№1. Найти производные функций:
а) 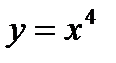 б)
б) 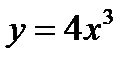 в)
в) 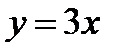 г)
г) 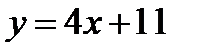
д) 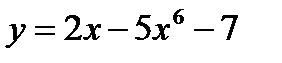 е)
е) 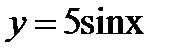 ж)
ж) 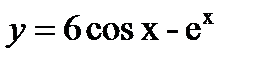 з)
з) 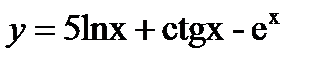
№2. Найти производную функции в точке:
а) 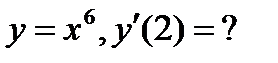 б)
б) 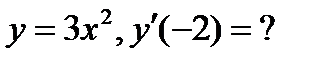 в)
в) 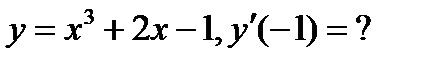
г) 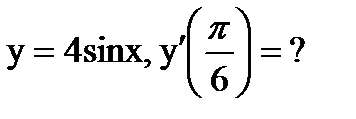 д)
д) 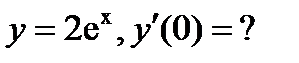 е)
е) 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|