Вариант 1. Вариант 2. Усечённый конус. Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

11 класс. Геометрия. 07. 02. 2022г.

Тема урока: Усеченный конус. Самостоятельная работа

Выполните самостоятельную работу (в рабочей тетраде)

Вариант 1

Образующая конуса равна 10 и наклонена к плоскости основания под углом 30 градусов. Найдите высоту конуса.

Высота конуса равна 10. Найдите образующую. если она наклонена к плоскости основания под углом 30 градусов.

Вариант 2

Радиус основания конуса равен 3, образующая наклонена к плоскости основания под углом 45 градусов. Найдите высоту конуса.
Высота конуса равна 6, образующая наклонена к плоскости основания под углом 45 градусов. Найдите диаметр конуса.

2. Теоретический материал для самостоятельного изучения

Итак, на прошлых уроках мы познакомились с понятием конуса, площади поверхности конуса. А сейчас познакомимся с понятием усеченного конуса.

Усечённый конус

Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

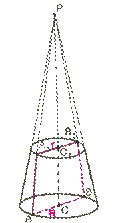
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

Элементы усеченного конуса:

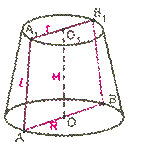
O — ось конуса и высота конуса.

A — образующая конуса.

Круги с центрами O и — основания усечённого конуса.

AO и 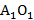— радиусы оснований конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось O 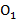конуса.

Осевое сечение конуса — это равнобедренная трапеция.

A 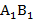B — осевое сечение конуса.

Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:

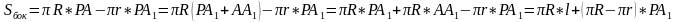
Так как Δ PAO∼ Δ PA1O1, то стороны их пропорциональны:

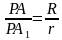
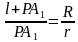
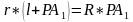
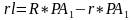
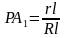
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:

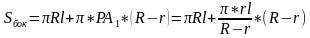
3. Решим вместе:

Задача 1: длины радиусов оснований и образующей усечённого конуса равны соответственно 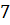см, см и см. Вычислите его высоту.

Решение: рассмотрим четырехугольник .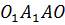

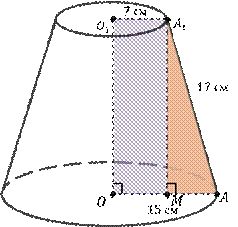
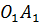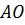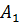Это есть прямоугольная трапеция с основаниями и . Высота этой трапеции и будет высотой нашего усечённого конуса . Для того чтобы её найти, проведём из точки меньшего основания перпендикуляр на большее основание трапеции 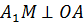. Фигура 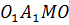является прямоугольником, значит противоположные стороны равны, т. е. 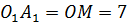(см), .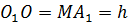

Рассмотрим . Он прямоугольный (по построению). Катет 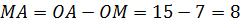(см). Применим теорему Пифагора и найдём длину катета 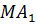. Получаем, что 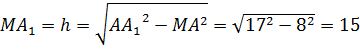(см).

Ответ: 15 см.

Задача 2: длины радиусов оснований усечённого конуса равны 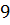см и см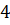. Вычислите площадь боковой поверхности этого конуса, если угол между образующей и плоскостью его основания равен .

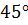Решение: запишем формулу для вычисления площади боковой поверхности усечённого конуса.

Рассмотрим четырёхугольник .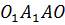

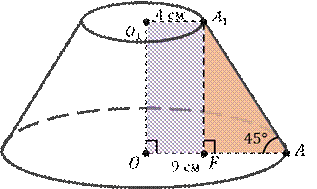
Это есть прямоугольная трапеция с основаниям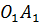и и 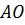. Высота этой трапеции и будет высотой нашего усечённого конуса .

Проведём из точки 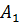меньшего основания перпендикуляр на большее основание трапеции 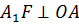. Фигура 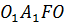является прямоугольником, значит, противоположные стороны равны, т. е. 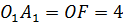(см), .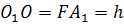

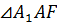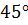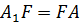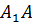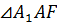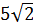Рассмотрим . Он прямоугольный (по построению). По условию задачи образующая усечённого конуса наклонена к его основанию под углом . Следовательно, катет . В свою очередь, . Применим теорему Пифагора и найдём длину гипотенузы треугольника . Получаем, что (см). Значит, образующая нашего усечённого конуса равна (см).

Подставим длины радиусов и образующей усечённого конуса в формулу для вычисления площади боковой поверхности. Посчитаем. Получим, что площадь боковой поверхности усеченного конуса равна (см 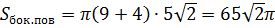²).

Ответ: 65 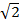π

4. Подведем итоги урока.

На этом уроке мы познакомились с понятием усечённого конуса. Узнали, что усечённым конусом называется часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной оси конуса. Назвали основные элементы усечённого конуса. А также вывели формулы для вычисления площади боковой поверхности и площади полной поверхности усечённого конуса.

5. Домашнее задание: Прочитать п. 63. Решить № 567, №568