Хелпикс

Главная

Контакты

Случайная статья



Практическое занятие . Решение тригонометрических уравнений (2 занятие). I. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. 1. Решение некоторых частных случаев простейших тригонометрических уравнений

Стр 1 из 2Следующая ⇒


 

 

 

Рассмотрено на заседании цикловой комиссии общетехнических и общеобразовательных дисциплин
Протокол № ____

от « » ____ 201__ года

Председатель цикловой комиссии
_______________ /Я. А. Прохоренко/

 
Математика


Практическое занятие   

Решение тригонометрических уравнений (2 занятие)

Цель:    Научиться  решать  тригонометрические уравнения.

         Познакомиться  с методами решения тригонометрических уравнений.

 

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:

1. Понятие уравнения.

2. Решение уравнения.

3. Понятие тригонометрического уравнения.

4. Решение тригонометрических уравнений.

 

I. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Опред. 1Простейшими тригонометрическими уравнениями являются уравнения вида:

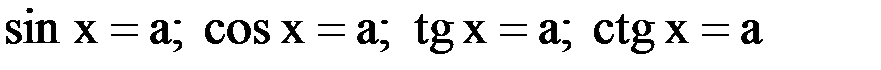
Опред. 2 Решить простейшее тригонометрическое уравнение - значит найти множество всех значений аргумента, при которых данная тригонометрическая функция принимает заданное значение а

Очень важно уметь решать простейшие тригонометрические уравнения, так как все способы и приемы решения любых тригонометрических уравнений заключаются в сведении их к простейшим.

 

 

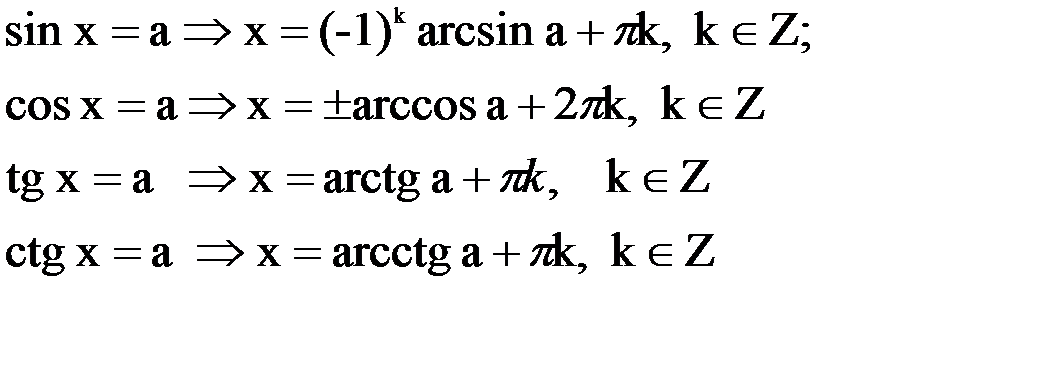
1. Решение некоторых частных случаев простейших тригонометрических уравнений

Множество решений каждого из следующих уравнений совпадает с нулями соответствующей тригонометрической функции:

 

 

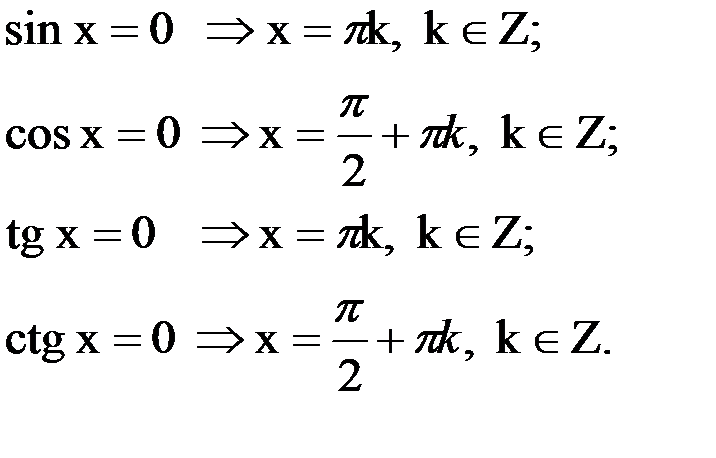
Множество решений каждого из следующих уравнений совпадает с множеством значений х, при которых соответствующая функция (синус или косинус) принимает наибольшее или наименьшее значение:

 

 

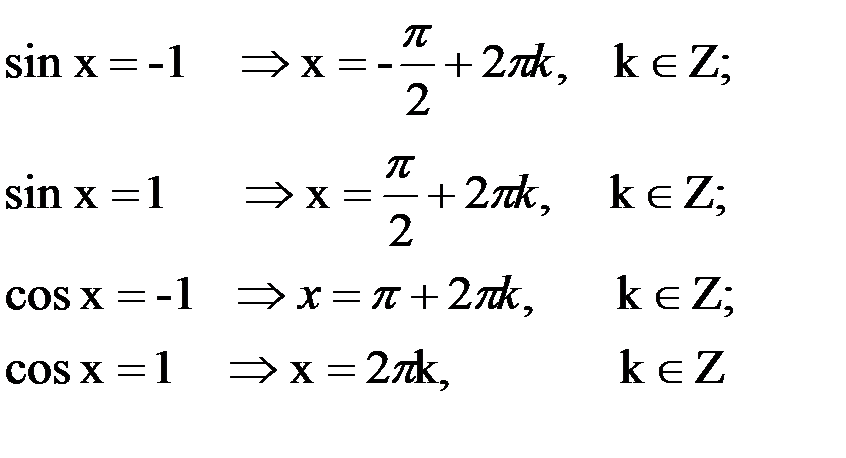
2. Решение уравнений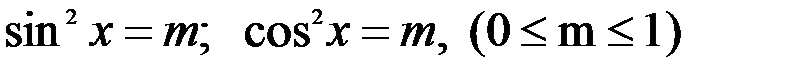

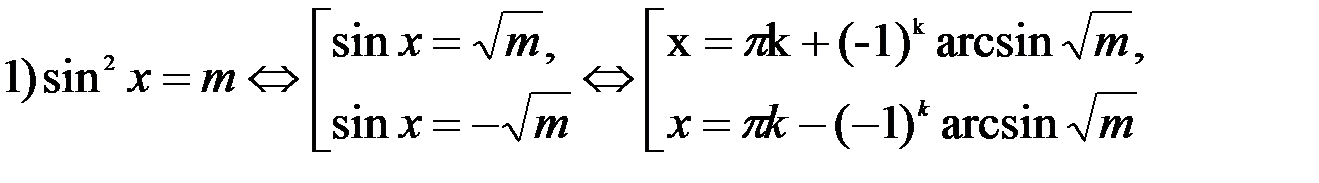
В этой записи решения множитель (-1)k, регулирующий знак вторых членов, является лишним. Если для некоторого целого k перед arcsin 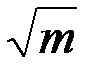в первой формуле берется знак плюс («+»), то для этого же k во второй – знак минус («-«), и наоборот(в зависимости от четности или нечетности k. Поэтому обе формулы можно объединить в одну, более простую:

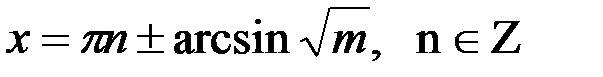
2)

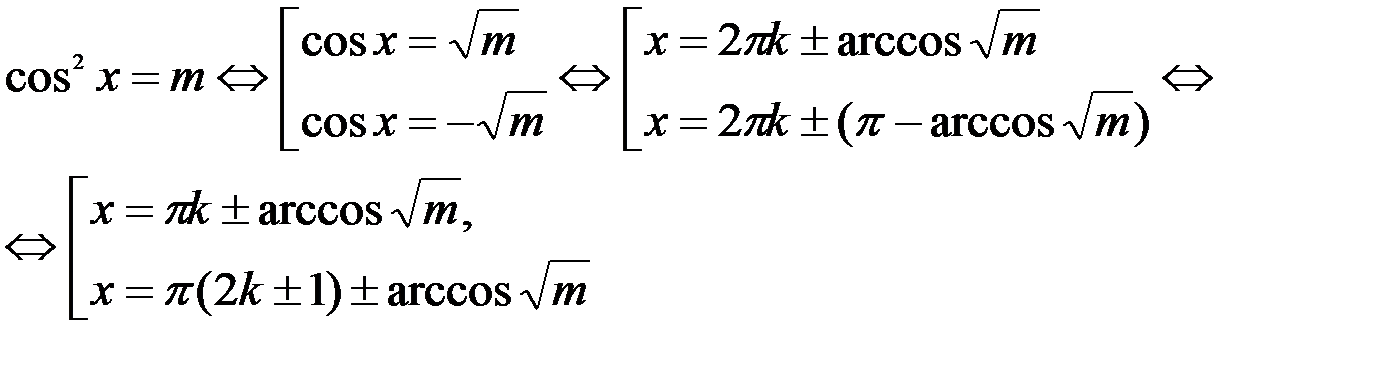
Объединив обе формулы, получим:

 

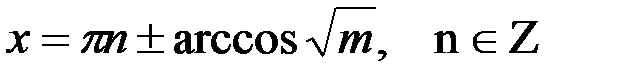
3. Решение уравнений

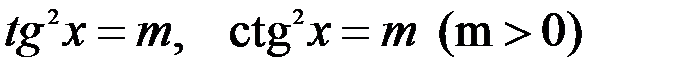
1)

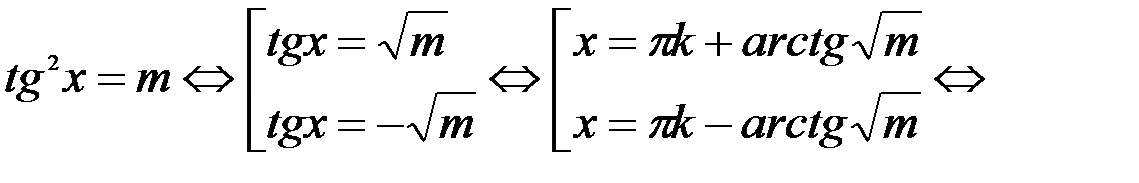
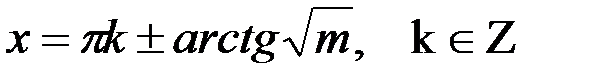
2) 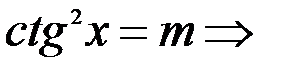аналогично находим:

 


12Следующая ⇒
  

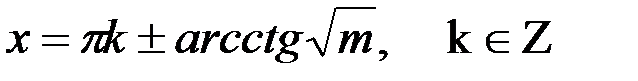
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.