Лабораторная работа №6. ГРАДУИРОВАНИЕ ТЕРМОЭЛЕМЕНТА. И ОПРЕДЕЛЕНИЕ ЕГО ТЕРМОЭ.Д.С.

Лабораторная работа №6

ГРАДУИРОВАНИЕ ТЕРМОЭЛЕМЕНТА

И ОПРЕДЕЛЕНИЕ ЕГО ТЕРМОЭ. Д. С.

Цель работы. Усвоение понятий о природе носителей заряда и термоэлектрических явлений

Задача: градуирование термопары

Приборы и принадлежности: термопара, нулевой гальванометр, два химических стакана, электроплитка, термометр, известное сопротивление на 100 или 200 Ом, соединительные провода.

Краткая теория.

В основе электронной теории проводимости металлов лежит представление о наличии внутри металла совокупности свободных электронов проводимости, образующих электронный газ. Газ окутывает ионную, положительно заряженную, кристаллическую решетку. Каждый его электрон совершает хаотическое движение между положительными ионами и иногда на короткое время выскакивает из пределов решетки на расстояния порядка 10^-8м.

С точки зрения этой теории можно объяснить возникновение разности потенциалов на границе соприкосновения двух различных металлов, имеющих различные температуры. В первом приближении свойства электронного газа можно уподобить свойствам идеального газа. Это дает нам возможность говорить о давлении электронного газа и для его расчета применить формулы, являющиеся выводами кинетической теории газов. Воспользуемся формулой p=nkT, где p-давление газа, k-постоянная Больцмана, n – число электронов, T – абсолютная температура.

Концентрация свободных электронов n₁ и n₂ в единице объема разных металлов разная. Это зависит от структуры атомов. У элементов с большим числом заряда ядра, а следовательно и электронов, внешние электроны легче переходят в свободную зону. Энергия ионизации также меньше у элементов первых групп периодической системы Менделеева. Поэтому при равных условиях у Cs и Fr концентрация свободных электронов много выше, чем у других металлов.

Концентрация свободных электронов также зависит от температуры. По классической теории при термодинамическом равновесии согласно распределению Больцмана-Максвелла заселенность возбужденных электронных уровней

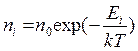
где n_o, n_i – заселенность нулевого и i− го уровней, E_i− энергия i− го уровня.

Однако на деле имеется распределение Ферми-Дирака:

Значения давления электронного газа в разных металлах, имеющих одинаковую температуру, будут неодинаковы. Это вызывает перемещение электронов из одного металла в другой. Тот металл, в который уходят электроны, будет заряжаться отрицательно, а тот, из которого уходят − положительно.

На границе соприкосновения, например, меди и железа движение электронов происходит от меди к железу. Между положительно заряженной медью и отрицательным железом возникает электрическое поле, создается разность потенциалов U= U_Fe - U_Cu (рис. 1).

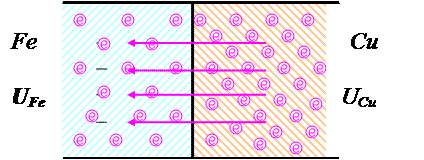Рис. 1

Когда разность давлений электронных газов уравнивается противодействиями электрического поля, перемещение электронов прекращается

Δ p=(n₁-n₂)k (1)

С повышением температуры газов разность давлений будет увеличиваться. Значит напряженность поля, которая должна его уравновешивать, увеличивается. В широких пределах часто разность потенциалов пропорциональна абсолютной температуре.

Возникновение эдс (термоэдс) в электрическом контуре, состоящем из двух проводников А и В, контакты между которыми поддерживаются при разных температуpax Т₁ и Т₂называется эффектом Зеебека.

Эффект 3еебека используется для прямого преобразования тепловой энергии в электрическую (термоэлектрогенераторы) и в термометрии.

Градиент температуры создает в проводнике градиент концентраций «холодных» и «горячих» носителей заряда. В результате этого возникают два диффузионных потока носителей — вдоль и против градиента температуры. Так как скорости диффузии и концентрации «горячих» и «холодных» носителей заряда различны, то на одном конце проводника создается избыточный положительный заряд, а на другом — отрицательный. Поле этих зарядов приводит к установлению стационарного состояния; число носителей, проходящих через поперечное сечение образца в обоих направлениях, одинаково. Возникающая диффузионная термоЭДС определяется температурной зависимостью концентрации носителей заряда и их подвижностью µ, обусловленной характером их взаимодействия с кристаллической решеткой, фононами, примесями и т. д.

В металлах электронный газ вырожден* и термоЭДС определяется только различием подвижностей «горячих» и «холодных» электронов.

* Внутри металла совокупность свободных электронов проводимости образует электронный газ. Уровни энергии электронов в газе подчинены так называемому распределению Ферми-Дирака:

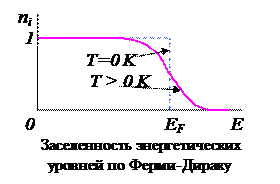
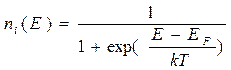
где E_F. − ферми− энергия, равная по значению химическому потенциалу φ . Электроны газа совершают хаотическое движение между положительными ионами, это движение ограничивается так называемой ферми-поверхностью.

При температуре Т = 0 К на этой поверхности находятся электроны с максимальной для -273°C энергией, которая называется ферми-энергией E_F. (рис. 1). При не слишком высоких температурах уровни сильно вырождены, и все нижние уровни заселены полностью − вероятность существования электрона с такой энергией равно единице (100%). При повышении температуры некоторые электроны могут выходить за пределы этой поверхности − границу. В узком интервале (порядка kT) около значения ферми-энергии вероятность заселенности уровней меняется плавно от 1 до нуля. Форма ферми-поверхности для разных металлов и сплавов различна, работа выхода электрона также различна. Вследствие разницы ферми− энергий возникает разность потенциалов на границе соприкосновения двух различных металлов − контактная электродвижущая сила, правда для металлов она незначительная

В полупроводниках термоЭДС обусловлена зависимостью от Т как подвижности, так и концентрации электронов и дырок. Обычно вклад втермоЭДС, связанный с температурной зависимостью концентрации * носителей, превышает вклад, обусловленный различием в подвижности µ(Т), хотя последний вполупроводниках (вследствие распределения носителей по Больцману) на несколько порядков больше, чем в металлах. Именно поэтому термоЭДС в полупроводниках значительно выше, чем в металлах.

*Концентрация носителей заряда зависит от температуры. В общем случае по классической теории при термодинамическом равновесии согласно распределению Больцмана-Максвелла заселенность возбужденных уровней экспоненциально растет при повышении температуры:

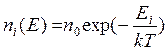
где n_o, n_i – заселенность нулевого и i− го уровней, E_i− энергия i− го уровня. Такому распределению соответствует концентрация носителей заряда в плазме, электролитах, полупроводниках и изоляторах.

ТермоЭДС контуpa определяется формулой:

, (1)

где α _A и α _В называются абсолютными термоЭДС проводников А и В, Абсолютная термоЭДС — характеристика проводника, равная α = dU/dT, где U — ЭДС, возникающая в проводнике при наличии в нём градиента температур.

Другое термоэлектрическое явление* — эффект Пельтье: выделение (или поглощение) тепла (в зависимости от направления тока) в местах контактов разнородных проводников.

Количество тепла Q пропорционально количеству электричества It, прошедшему через контакт:

Q = π I t, (2)

где I —сила тока, t — время, π — коэффициент Пельтье.

Как термоэлектрическое явление рассматривается эффект Томсона: выделение (или поглощение) тепла в объеме проводника при протекании тока (в дополнение к теплоте Джоуля), если вдоль проводника существует перепад температур:

Q= ρ (Т₁ — Т₂) I t, (3)

где Т₁, Т₂ — температуры на концах проводника, ρ — коэффициент Томсона. Томсон вывел термодинамические соотношения между α, π, ρ :

π = α Т, 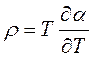(4)

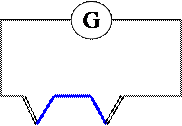Если два куска разных металлов (алюминий и железо) спаять как на рис. 2, то в местах спаев возникает разность потенциалов, причем на первом спае разность потенциалов направлена противоположно по отношению к разности потенциалов на втором спае. В результате имеем ноль.

Рис. 2 Если один из спаев нагреть до T₂,, а другой останется при T₁, то разности потенциалов U₂и U₁, возникающие на разных спаях, не будут уравновешивать друг друга, в цепи возникает ЭДС, равная E = U₂- U_1. Тогда в цепи пойдет электрический ток. U₂ и U₁ примерно пропорциональны абсолютным температурам. Поэтому возникающую ЭДС называют термоэлектродвижущей силой. ЭДС пропорциональна разности абсолютных температур:

E = α ( T₂-- T₁) или E = α ( t₂-- t₁) (5)

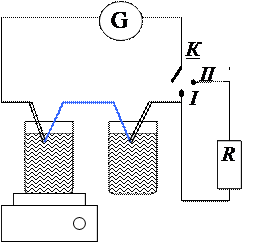
Рис. 3

Можно считать, что термоЭДС есть линейная функция разности температур спаев. Однако для многих металлов зависимость E от t₂− _-t₁имеет более сложный характер и только при небольших разностях температуры сохраняется точная линейность этой зависимости. При практическом использовании термопары* обычно не выходят за пределы линейной зависимости от t₂- t₁ и данную термопару характеризуют величиной α из формулы (5). Как видно из этой формулы, величина α численно равна термоэлектродвижущей силе, возникающей в термопаре при разности температур спаев в 1 градус.

* ТЕРМОПАРА — датчик температуры. состоящий из двух соединённых между собой разнородных электропроводящих элементов (обычно из металлических проводников, реже из полупроводников) Действие термопары основано на эффекте Зеебека. Если контакты (обычно спаи) проводящих элементов, образующих термопару (их часто называют термоэлектродами), находятся при разных температурах, то в цепи термопары возникает ЭДС, величина которой однозначно определяется температурами горячего и холодного контактов и природой материалов, применённых в качестве термоэлектродов.

ЭДС термопары из металлических проводников обычно лежит в пределах 5—60 мкВ/К. ЭДС термопары из полупроводников может быть на порядок выше. Точность определения температуры с помощью термопары составляет, как правило, нескольких К (градусов), а у некоторых термопар достигает 0, 01 К.

Термопары используются в самых различных диапазонах температуры (от нескольких К до примерно 2800 К), Применяются в устройствах для измерения температуры и различных автоматизированных системах управления и контроля. В сочетании с электроизмерительными приборами (милливольтметром, потенциометром и т. п. ) термопара образует термоэлектрический термометр.

Задачей настоящей работы является градуирование термопары, т. е. установление действительной зависимости термоЭДС этой термопары от разности температур и определение α в пределах линейного участка. На рис. 3 дана схема установки, используемой при выполнении работы. Один конец термопары присоединяется к гальванометру. Переключатель дает возможность включать в цепь и выключать сопротивление R Спаи термопар А и В погружают в стаканы с водой. Туда же опускают термометр. Отсчитывают значение комнатной температуры t₁

Один из стаканов ставят на электроплитку. При положении переключателя К в положение I через гальванометр течет ток:

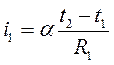(6)

где R₁ - неизвестное сопротивление цепи, состоящей из термопары и гальванометра.

При положении переключателя К в положение II (при той же разности температур) подключается дополнительное известное сопротивление R, и гальванометр покажет ток:

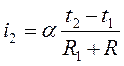(7)

Из уравнений (6) и (7), исключая неизвестное сопротивление, получим

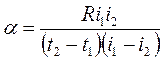(рабочая формула) (8)

Указания к выполнению работы:

1. Подготовить таблицу экспериментальных данных:

t₁	t₂°С
	i₁, А
	i₂, А
	α
	Среднее значение α

2. Погрузить термопары в чайники с водой, имеющие одинаковую температуру t₁. При этом в цепи тока не будет. (по гальванометру в обеих положениях переключателя значение силы тока должно быть =0).

3. Значение t₁ измерить с помощью термометра и записать в таблицу.

4. Включить чайник на 10 сек. и выключить. Температура после этого все еще будет подниматься. Когда температура установится (через 5 мин. ), записать значение t₂. Затем только снять показания гальванометра в двух положениях переключателя К. Зная цену деления гальванометра, найти для каждого измерения силу тока в амперах.

5. Снова включить чайник. Посчитав 5 сек., выключить. Через 3-5 мин записать установившуюся температуру, и снять показания гальванометра в двух положениях переключателя К. Повторить задание 8 раз.

6. Остывание: при тех же значениях температуры снять показания гальванометра в двух положениях переключателя.

7. Построить график зависимости E=f(Δ t).

8. Найти значение удельного термоЭДС, рассчитывая его по данным отдельных измерений. Вычислить среднее значение:

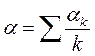, k = 1, 2, 3, …n.

Контрольные вопросы:

1. Эффект Зеебека

2. Эффекты Пельтье и Томсона

3. Взаимосвязь между коэффициентами Зеебека, Пельтье и Томсона

4. «Холодные» и «горячие» заряды

5. ТермоЭДС подвижности носителей заряда

6. Контактная термоЭДС

7. ТермоЭДС в металлах

8. ТермоЭДС в полупроводниках

9. Термопара

10. Применение термопары и термоэлементов.

Литература:

1. Калашников С. Г. Электричество. М.: Наука, 1985, с. 198-202, 422-435.

2. Сивухин Д. В. Электричество. М.: Наука, 1977, с. 104-107, 476-497.