КОНСУЛЬТАЦИЯ 17.05 – самостоятельная №2 Теория

Стр 1 из 2Следующая ⇒

КОНСУЛЬТАЦИЯ 17. 05 – самостоятельная №2 Теория

Машинное обучение. Регрессия. Теория.

Сразу отвечаем на вопросы:

Да, постараемся сделать запись.

Да, файлы вывесим в группу.

О чем сегодня говорим?

1. Машинка: максимальное общие сведения.

2. Отличие регрессии от классификации.

3. Регрессия: что, как, зачем.

4. Очень подробно про метрики.

5. Линейная регрессия.

6. Обобщающая способность.

7. Работа с фичами.

Линейная регрессия.

Одна из самых простых моделей машинного обучения.

В простейшем виде ( это когда прогнозируем по одному признаку) выглядит так:

ŷ = w0 + w1*x1

Где, напоминаем:

x – признак какого-то объекта

y – целевая переменная

w1 – параметр (или вес)

w0 – параметр (или вес)

Это, в принципе, то же самое, что и известная нам из математики y = kx+b

Линейной мы её называем, потому что мы пытаемся провести через облако точек линию. Как, например, тут:

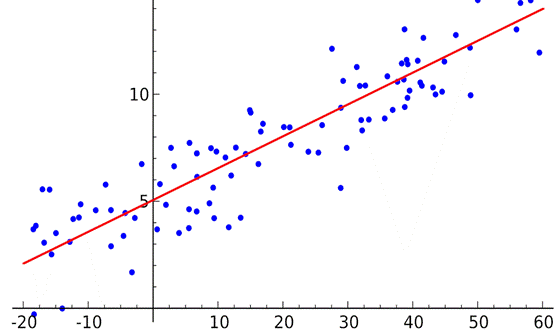
Все наши прогнозы – красная линия. Синие – реальные значения.

Мы можем прогнозировать и по нескольким признакам:

ŷ = w0 + w1*x1+w2*x2+... +wn*xn

В таком случае формула станет просто длиннее и страшнее, но обозначения всё те же.

И как же всё находить?

Это всё конечно хорошо, но пока совершенно непонятно, что с этим делать на практике. Логично, что нам для решения задачи нужно, условно, провести такую “красную линию” чтобы она была удалена от всех “синих точек” на минимальное расстояние.

Если же в общем, то мы просто пытаемся найти такие w (параметры/веса), чтобы результаты предсказаний по этой функции (y) были наиболее близки к правде.

Выразим эти слова в математической формуле:

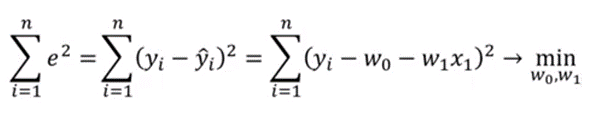
у с “крышечкой” это факт, а просто у это прогноз.

е это error, то есть, ошибка. Логично, что она должн быть минимальной.

Почему квадрат?

1. Чтоб не потерять отрицательные значения

2. Чтоб было масштабнее

12 Следующая ⇒