
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сложное движение точки
Основные понятия и определения
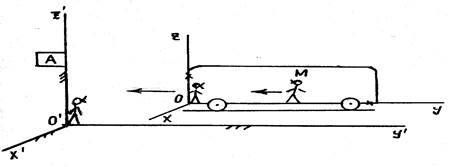
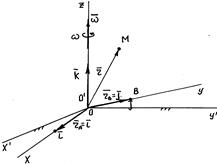
Пусть твердое тело с движущейся по нему точкой М совершает движения по отношению к некоторой неподвижной системе отсчета (o’x’y’z’).
Введем дополнительную подвижную систему отсчета, жестко скрепленную с движущимся телом (oxyz).
Определение 1.
Абсолютным называется движение( траектория, скорость, ускорение) точки относительно неподвижной системы отсчета.
Абсолютное движение фиксирует наблюдатель, связанный с неподвижной системой отсчета.
Vα - абсолютная скорость,
α α - абсолютное ускорение,
Sα - абсолютная траектория.
Определение 2.
 Относительным называется движение (траектория, скорость, ускорение) точки относительно подвижной системы отсчета.
Относительным называется движение (траектория, скорость, ускорение) точки относительно подвижной системы отсчета.
Относительное движение фиксирует наблюдатель, связанный с подвижной системой отсчета.
Vr - относительная скорость,
α r - относительное ускорение,
Sr - относительная траектория.
«r» лат. relativus-относительный
Определение 3.
Переносным называется движение подвижной системы отсчета и всех неизменно связанных с ней точек относительно неподвижной системы отсчета.
Для восприятия понятий переносной скорости и ускорения дадим определение геометрической среды.
Неизменяемой геометрической средой называется совокупность геометрических точек неизменно связанных с подвижной системой отсчета и движущихся вместе с ней.
Переносной скоростью и переносным ускорением называется скорость и ускорение той точки геометрической среды, с которой в данный момент совпадает движущаяся точка.
V e-переносная скорость,
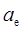 - переносное ускорение,
- переносное ускорение,
S e- переносная траектория.
«e» фр. entrainair-увлекать с
Теорема сложения скоростей в сложном движении
Теорема. Абсолютная скорость в сложном движении точки равна геометрической сумме относительной и переносной скоростей.
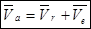
Доказательство. Пусть точка М совершает сложное движение. За время 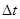 точка переместится по относительной траектории в положении М1, а по переносной – в М2.
точка переместится по относительной траектории в положении М1, а по переносной – в М2.
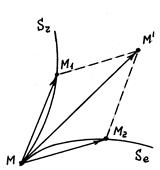
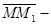 вектор относительного перемещения точки,
вектор относительного перемещения точки,
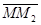 - вектор переносного перемещения точки,
- вектор переносного перемещения точки,
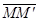 -вектор абсолютного перемещения точки.
-вектор абсолютного перемещения точки.
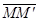 =
= 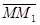 +
+ 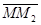
Поделим на 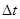
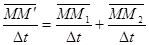 - средняя скорость.
- средняя скорость.
Перейдем к пределу
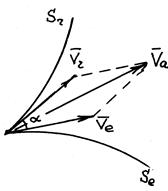
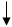
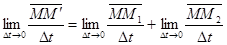

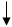
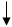

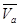 =
= 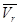 +
+ 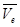
Теорема доказана.
Модуль. Если 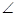 между
между 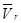 и
и 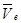
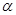 , то
, то
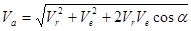 ;
;
по методу проекций 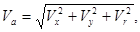 где
где 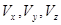 - проекции
- проекции 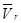 и
и 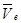 на оси координат.
на оси координат.
Теорема сложения ускорений при переносном поступательном движении
Теорема. При переносном поступательном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений
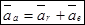
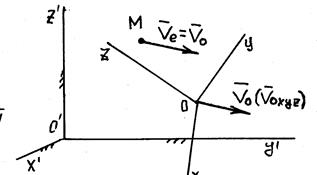
Доказательство. Пусть точка М совершает сложное движение относительно неподвижной системы отсчета o’x’y’z’.
Введем подвижную систему отсчета oxyz, совершающую поступательное движение. Точка М вместе с подвижной системой отсчета также совершает поступательное движение.
Продифференцируем по t векторное равенство 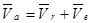
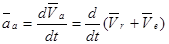 ,
,
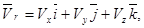 где
где 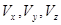 -проекции относительной скорости
-проекции относительной скорости 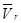 на оси координат,
на оси координат,
|
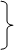
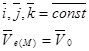 т. к. подвижная система совершает поступательное
т. к. подвижная система совершает поступательное
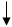

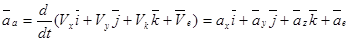 ,
,
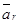
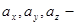 проекции относительного ускорения
проекции относительного ускорения 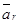 на оси координат.
на оси координат.
Т. о. 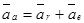 - теорема доказана.
- теорема доказана.
Модуль. 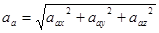 , где
, где 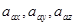 проекции векторов
проекции векторов 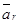 и
и 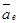 на оси координат.
на оси координат.
Задача. Кулиса ВС кривошипно-кулисного механизма приводного молота приводится в возвратно-поступательное движение кривошипом ОА длиной 1, 2 м. Кривошип имеет в данный момент угловую скорость 2 с-1 и угловое замедление 0, 5 с-2. Найти скорость и ускорение молота, когда кривошип ОА будет образовывать угол 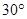 с вертикалью.
с вертикалью.
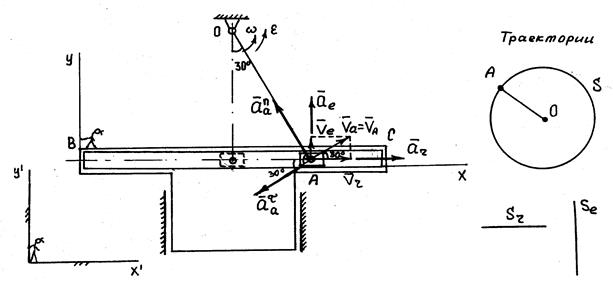
Дано:
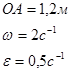
Найти:
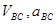
Решение
По теореме сложения скоростей
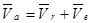 (1)
(1)
или 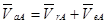
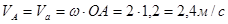 , (
, (  ).
).
Спроецируем векторное равенство (1) на ось y:
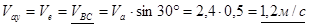 .
.
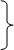
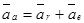
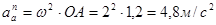 ,
,
или 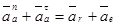 (2)
(2) 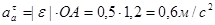 .
.
Спроецируем вектор равенства (2) на ось y:
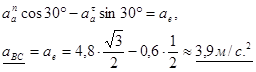
Ответ: 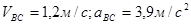 .
.
Теорема сложения ускорений при переносном вращательном движении (Теорема Кориолиса)
Густав Кориолис, французский ученный, 1792-1843 г. г.
 Теорема. При переносном вращательном движении абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова (поворотного) ускорений
Теорема. При переносном вращательном движении абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова (поворотного) ускорений
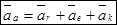
Доказательство. Пусть точка М совершает сложное движение относительно неподвижной системы отсчета o’x’y’z’. Введем дополнительную систему отсчета, совершающую вращательное движение. Точка М вместе с подвижной системой также совершает вращательное движение.
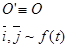
Продифференцируем по t векторное равенство


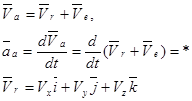
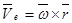 - по формуле Эйлера
- по формуле Эйлера
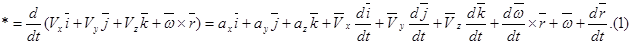 Выполним анализ входящих в (1) величин (векторов) и их произведений.
Выполним анализ входящих в (1) величин (векторов) и их произведений.
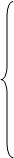 1.
1. 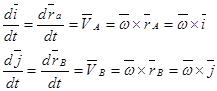
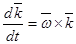 (= О, т. к. вектора коллинеарны; в общем случае
(= О, т. к. вектора коллинеарны; в общем случае 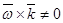 ),
),
В нашем случае система отсчета совершает вращательное движение.
2. 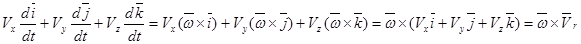 .
.
3. 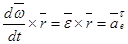 .
.
4. 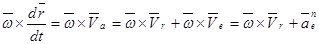 .
.
Итак, 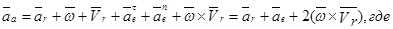
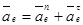
Обозначим 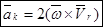 (2) - кориолисово (поворотное, добавочное) ускорение.
(2) - кориолисово (поворотное, добавочное) ускорение.
Читать. Ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки.
Таким образом, абсолютное ускорение точки выразится следующим образом:
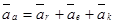 , что и требовалось доказать.
, что и требовалось доказать.
Или в развернутом виде
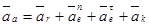


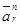
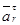
Модуль | 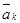 |
| 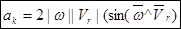
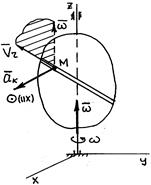
Направлен вектор 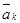 согласно (2) перпендикулярно плоскости, содержащей вектора
согласно (2) перпендикулярно плоскости, содержащей вектора 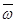 и
и 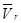 , в ту сторону, откуда поворот от
, в ту сторону, откуда поворот от 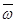 до
до 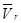 на кратчайший угол виден происходящим против часовой стрелки.
на кратчайший угол виден происходящим против часовой стрелки.
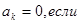
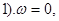
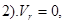
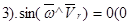 или
или 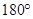
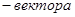
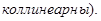
Правило Жуковского
При сложном движении точки в одной плоскости направление вектора 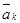 можно определить поворотом вектора
можно определить поворотом вектора 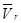 в сторону вращения (переносного)
в сторону вращения (переносного) 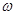 тела на
тела на 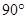 .
.
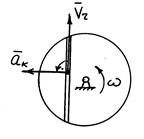
Модуль в этом случае
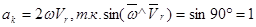 .
.
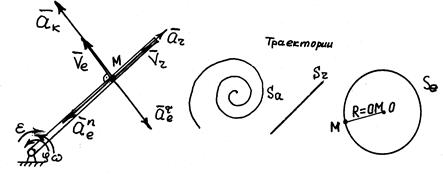
Задача. Вдоль трубки, вращающейся согласно уравнению 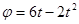 , движется точка М по закону
, движется точка М по закону 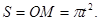 В момент времени
В момент времени 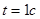 определить абсолютные скорость и ускорение точки.
определить абсолютные скорость и ускорение точки.
Дано:
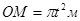
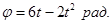
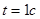
Найти:
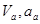
Решение
Рассмотрим движение точки М. Относительное движение - вдоль трубки; переносное - вместе с трубкой.
1. Определим положение точки М при 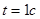
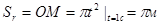
2. Определитм абсолютную скорость точки М.
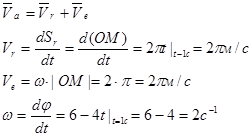
т. к 
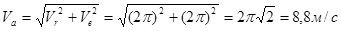 ,
,
или по методу проекций
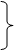
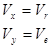
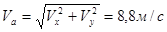 .
.
3. Определим абсолютное ускорение точки М.
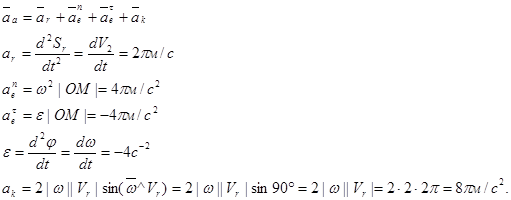
По методу проекций найдем модуль абсолютного ускорения:
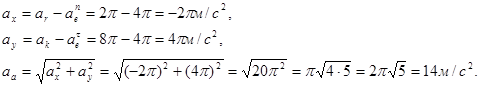
Ответ: 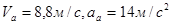 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|