
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа. Комплексные числа и действия над ними.. Задание 1. Тест.. Задание 2. «Магическая таблица».
Практическая работа
Комплексные числа и действия над ними.
Цель работы: закрепить навыки выполнения действий с комплекснымичислами
Задание 1. Тест.
№1. Комплексными числами называются числа вида x+yi, где i- мнимая единица, а x и y -
1) целые числа
2) натуральные числа
3) действительные числа
4) рациональные числа
№2. Модуль комплексного числа z=x+yi равен
1) 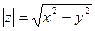
2) 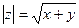
3) 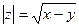
4) 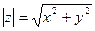
№3. Какое число является комплексно-сопряженным числу z=x+yi
1) z=-x+yi
2) z=x-yi
3) z=-x-yi
4) z=x+yi
№4. Сумма двух комплексных чисел z1=a+bi и z2=c+di равна
1) (a + bi ) + (c + di ) = (a + c) + (b + d)i
2) (a + bi ) + (c + di ) = (a + c) - (b + d)i
3) (a + bi ) + (c + di ) = (a - c) + (b - d)i
4) (a + bi ) + (c + di ) = (a + d) + (b + c)i
№5. Произведение двух комплексных чисел z1=a+bi и z2=c+di равно
1) (a + bi ) * (c + di ) = (ac – bd) - (bc + ad)i
2) (a + bi ) * (c + di ) = (ac – bd) + (bc + ad)i
3) (a + bi ) * (c + di ) = (ac + bd) + (bc + ad)i
4) (a + bi ) * (c + di ) = (ac + bd) - (bc + ad)i
№6. Тригонометрическая форма комплексного числа z=a+bi имеет вид
1) 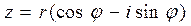
2) 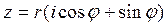
3) 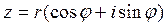
4) 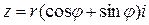
№7. Разность двух комплексных чисел z1=a+bi и z2=c+di равна
1) (a + bi ) - (c + di ) = (a + c) - (b + d)i
2) (a + bi ) - (c + di ) = (a - c) + (b - d)i
3) (a + bi ) - (c + di ) = (a - c) + (b + d)i
4) (a + bi ) - (c + di ) = (a - d) + (b - c)i
№8. Действительная и мнимая части числа z=3-2i равны
1) Re z= 3 Im z= -2
2) Re z= 3 Im z= 2
3) Re z= 2 Im z= -3
4) Re z= -2 Im z= 3
Задание 2. «Магическая таблица».
С помощью таблицы узнайте имя итальянского алгебраиста, предложившего в 1545 ввод числа новой природы. Для этого необходимо прочесть буквы, образованные пересечением номера столбца и номера строки.
0 1+3i 2+2i 3+i 2+0i 2+i 1 3+3i 3i
3 2+3i 2i 3+2i 1+i i 1+2i
| Действительная часть числа | |||||
| Мнимая часть числа | |||||
| д | а | о | к | ||
| н | а | л | р | ||
| р | о | и | д | ||
| o | ж | а | м | ||
Задание 3. Произведите арифметические действия над комплексными числами и узнайте, имяфранцузского математика, который в конце 18 века смог сказать, что математический анализ уже не затрудняют мнимые величины
1) (3 + 5i) + (7 – 2i).
2) (6 + 2i) + (5 + 3i).
3) (– 2 + 3i) + (7 – 2i).
4) (5 – 4i) + (6 + 2i).
5) (3 – 2i) + (5 + i).
6) (4 + 2i) + (– 3 + 2i)
7) (– 5 + 2i) + (5 + 2i).
Л=10-2i ж=4i а=8-i г=5+i р=11-2i н=1+4i а=11+5i Задание 4. Произведите арифметические действия над комплексными числами [3, 206-207] и узнайте, имя ученого, предложившего изображать комплексное число точкой на координатной плоскости.
1. ___ (2 + 3i)(5 – 7i). =
2. ___(6 + 4i)(5 + 2i)=
3. ___(3 – 2i)(7 – i). =
4. ___ (– 2 + 3i)(3 + 5i)=
5. ___(1 –i)(1 + i)=
6. ___ (3 + 2i)(1 + i)=
7. ___(6 + 4i)3i=
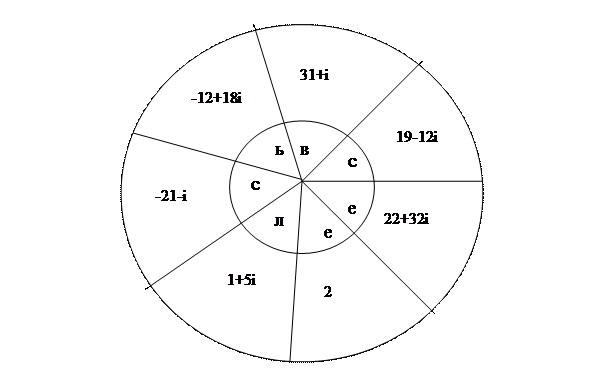
Задание 5. Самостоятельная работа.
Записать в тригонометрической форме комплексное число.
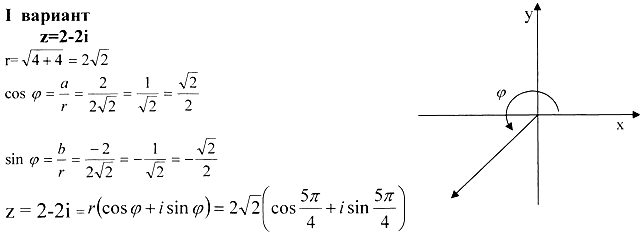
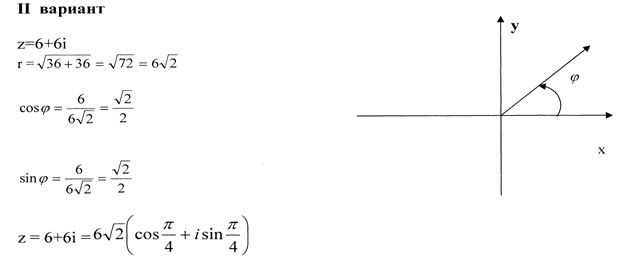
Записать полученный результат в показательной форме
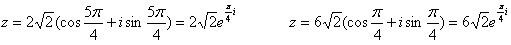
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|