Понедельник 20.04.20 и вторник 21.04 ( два урока)

Понедельник 20. 04. 20 и вторник 21. 04 ( два урока)

7 класс алгебра

Тема: Системы линейных уравнений с двумя переменными.

Цель:

I. Повторение, устная работа.

Ответ на третий вопрос ищи в учебнике на стр. 78, и заметим, что если угловые коэффициенты 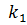= 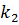, а числа 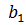≠ 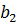, то прямые параллельны и различны, а если 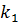= 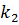и числа 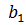= 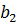, то прямые сливаются в одну прямую.

II. Изучение нового материала.

1) Изучи п. 42 на стр. 207. Рассмотри задачу о числах. Нам понятно, что для решения задачи составили два уравнения с двумя неизвестными, и надо найти одно общее для двух уравнений решение. Говорят, что составили систему двух уравнений с двумя неизвестными. Надо найти общее решение этих уравнений. Говорят, что надо решить систему.

2) Запомни, как записывается система двух уравнений с двумя переменными и что называется решением системы. (см. стр. 208). Решить систему уравнений означает, что надо найти ее решение или доказать, что решения нет. Есть и такие системы.

3) На стр 208 поясняется, что систему можно решать графически, т. е. при помощи графиков уравнений. Для этого в одной координатной плоскости строят графики первого и второго уравнения системы. Координаты точки пересечения графиков ( пара чисел, которые мы определяем по чертежу), дают значения неизвестных, которые и надо было определить, т. е. мы находим решение системы при помощи графиков (решаем графически). Однако, этот способ часто позволяет найти решение системы лишь приближенно. Но зато позволяет точно дать ответ на вопрос, имеет ли система решение или нет, и сколько решений она имеет.

4) Разбери решение примера 1. 2. 3 на стр. 208 – 209. Сделай такой вывод и запомни его: чтобы дать ответ на вопрос имеет ли система решение или нет, надо:

1°. Выразить у из каждого уравнения системы через х, т. е. записать уравнения в виде у = kx + b, и сравнить значения угловых коэффициентов k и значения свободных членов b.

2°. Если угловые коэффициенты не равны, , то прямые пересекаются, значит, система имеет единственное решение.

3°. Если угловые коэффициенты равны, 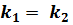и 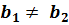, то прямые параллельны, точки пересечения нет и, значит, система не имеет решения.

4°. Если угловые коэффициенты равны, 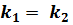и 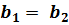, то прямые сливаются в одну прямую, все точки у прямых общие, значит, система имеет бесконечно много решений.

12 Следующая ⇒