Линейно зависимые и линейно независимые векторы

Разложение вектора по ортам координатных осей

Определение

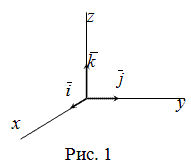
Система ортов (или базисная система векторов) - это системаединичных векторов

осей координат.

Орт координатной оси 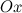обозначается через , оси 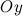- через 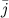, оси - через 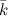(рис. 1).

Для любого вектора 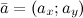, который лежит в плоскости 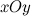, имеет место следующее разложение:

Если вектор 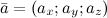расположен в пространстве, то разложение по ортам координатных осей имеет вид:

Пример

Задание. Зная разложение 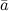по базисной системе векторов: 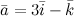, записать координаты этого вектора в пространстве.

Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что 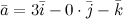, получаем, что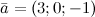

Пример

Задание. Вектор 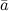задан своими координатами: 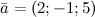. Записать разложение данного вектора по ортам осей координат.

Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе, поэтому искомое разложение:

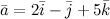
Линейно зависимые и линейно независимые векторы

Определение

Линейной комбинацией векторов 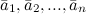называется выражение вида:

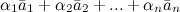где 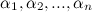- произвольные числа.

Определение

Линейная комбинация 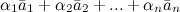называется тривиальной, если все коэффициенты 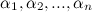равны нулю одновременно: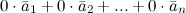

Линейная комбинация 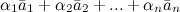называется нетривиальной, если хотя бы один из коэффициентов 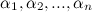отличен от нуля.

Определение

Ненулевые векторы 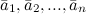называются линейно зависимыми, если нетривиальная линейная комбинация этих векторов равнанулевому вектору: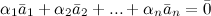

Пример

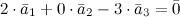
Определение

Ненулевые векторы 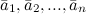называются линейно независимыми, если только тривиальная линейная комбинация этих векторов равна нулевому вектору.

Пример

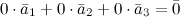
Свойства линейно зависимых векторов:

1. Если два вектора линейно зависимы, то они коллинеарны. Верно и обратное утверждение.

2. Если три вектора линейно зависимы, то они компланарны. Верно и обратное.

3. Четыре произвольных вектора всегда линейно зависимы.