2 способ (короткий)

2 способ (короткий)

Если 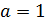, то уравнение является линейным. Тогда оно принимает вид 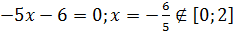. Значит, 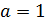не подходит.

При 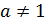уравнение является квадратным.

Рассмотрим функцию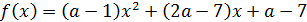

При 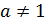данная функция является квадратичной

Вычислим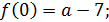

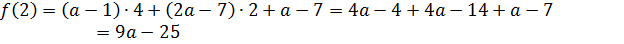
Уравнение будет иметь в точности один корень на отрезке 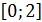тогда и только тогда, когда функция принимает значения разного знака на концах отрезка. Таким образом

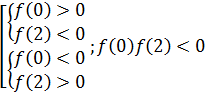
Отдельно имеет смысл проверить случаи, когда 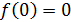и

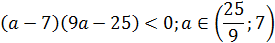
При получим .

Значит, подходит.

При 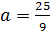получим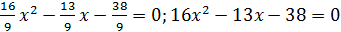

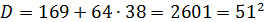
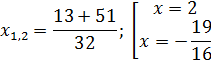
Значит, 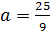подходит.

Ответ: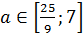

Замечание: рассмотрение крайних случаев можно слегка упростить (подумайте как)

Вывод – имеет смысл искать наиболее короткий способ решения и избегать буквальных, если это конечно возможно

Задача для самостоятельного решения

Найти все значения параметра 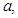при которых уравнение 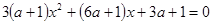имеет на отрезке 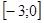единственный корень?

Попробовать придумать идеологию нескольких методов решения и реализовать наиболее оптимальный из них (а лучше – несколько! )

⇐ Предыдущая 12