Тема занятия: Вычисление расстояний в пространстве.

Цель: Научиться изображать расстояние от точки до плоскости.

Расстояние от точки до плоскости треугольника удобно рассматривать с помощью пирамид.

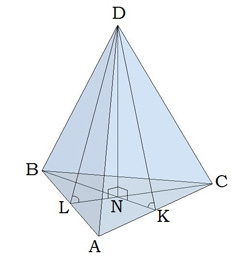
Задача 1.

Расстояние от точки D до плоскости ABC изображается отрезком DN. Рисуется он вертикально. Считается, что DN перпендикулярен плоскости треугольника АВС.

Задача 2.

Расстояние от точки D до вершины А треугольника ABC изображается отрезком DА.

Из точки А проведен перпендикуляр AD.

Расстояние от концов перпендикуляра DА до противоположной стороны треугольника характеризуется отрезками АЕ и DE. Длины этих отрезков находятся из прямоугольных треугольников.

На рисунке дана треугольная пирамида с ребром DA, перпендикулярным основанию.

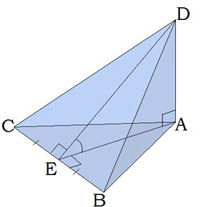
DA — перпендикулярное основанию ребро, DA также является высотой,

Δ DAC и Δ DAB — прямоугольные, угол DEA — двугранный угол при основании.

Задача 3.

Провести перпендикуляр от вершины прямоугольника.

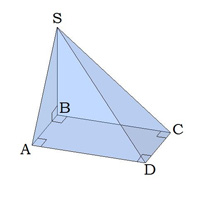
Отрезок SB перпендикулярен прямоугольнику ABCD.

SB также является высотой, полученной пирамиды.

Δ SBA и Δ SBC— прямоугольные;

если основание — прямоугольник, то Δ SAD и SCD — прямоугольные.

(Дополнительная информация:

Пирамида, основанием которой является правильный многоугольник, а вершина которой проецируется в центр основания, называется правильной пирамидой.

Боковые грани правильной пирамиды — равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды называется апофемой.

Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром.

Все грани тетраэдра — равные равносторонние треугольники. )