
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
(Признак сравнения). (Предельный признак сравнения). (Признак Коши). Признак Лейбница. Если члены ряда ( 3 ) последовательно убывают (un > un+1 )и стремятся к 0 ( lim un = 0 при n ® ¥ ),то ряд сходится, причем, его сумма S > 0иS < u1.. S2m =
| 1 Вопрос Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения. Общим решениемдифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество. Свойства общего решения. 1) Т. к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений. 2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0). Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения. | 2 Вопрос
Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т. е. соотношение вида:
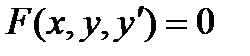 Если такое соотношение преобразовать к виду
Если такое соотношение преобразовать к виду 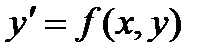 то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Задачей Кошиназывается нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Задачей Кошиназывается нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную 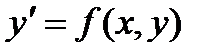 , то какова бы не была точка (х0, у0) в области D, существует единственное решение , то какова бы не была точка (х0, у0) в области D, существует единственное решение 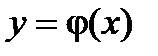 уравнения уравнения 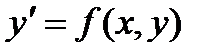 , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т. е. существует единственное решение дифференциального уравнения.
Геометрический смысл теоремы
Существует и при том ед функция y=фи(x), график кот проходит чз точку y0, x0 и явл решением диф ур-я
Условие, что при х=х0 и функция у=у0 наз-т нач. условиями
Общим решением диф ур-я 1-го порядка наз-ся функция у=фи(х, С), где С-конст, удовл. Условиям:
1)она уд-т диф-му ур-ю при любом конкр значении пост С
2)каково бы ни было нач усл, можно найти такое значение С=С0, что ф-ция у=фи(х, С0) удовл данному нач условию
При реш диф ур-ий часто получ соотношение Ф (х, н, С)=0 неявно задающее ф-цию у – это общ решение, а такое соотношение – общий интегралл диф ур-я
Если в общем решении у=фи(х, С), константе С придать конкр значение С=С0, то это – частное решение
Если треб-ся найти частн решение диф ур-я, кот уд-т ее нач усл, то говорят что задана задача Коши
Полученное решение – это решение задачи Коши , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т. е. существует единственное решение дифференциального уравнения.
Геометрический смысл теоремы
Существует и при том ед функция y=фи(x), график кот проходит чз точку y0, x0 и явл решением диф ур-я
Условие, что при х=х0 и функция у=у0 наз-т нач. условиями
Общим решением диф ур-я 1-го порядка наз-ся функция у=фи(х, С), где С-конст, удовл. Условиям:
1)она уд-т диф-му ур-ю при любом конкр значении пост С
2)каково бы ни было нач усл, можно найти такое значение С=С0, что ф-ция у=фи(х, С0) удовл данному нач условию
При реш диф ур-ий часто получ соотношение Ф (х, н, С)=0 неявно задающее ф-цию у – это общ решение, а такое соотношение – общий интегралл диф ур-я
Если в общем решении у=фи(х, С), константе С придать конкр значение С=С0, то это – частное решение
Если треб-ся найти частн решение диф ур-я, кот уд-т ее нач усл, то говорят что задана задача Коши
Полученное решение – это решение задачи Коши
| 3 Вопрос
А) Дифференциальное уравнение
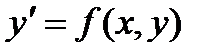 называется уравнением с разделяющимися переменными, если его можно записать в виде
М(х)dx=N(y)dy
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Б) Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде: называется уравнением с разделяющимися переменными, если его можно записать в виде
М(х)dx=N(y)dy
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Б) Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
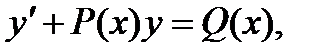 при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.
P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.
В) Уравнением Бернуллиназывается уравнение вида
при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.
P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.
В) Уравнением Бернуллиназывается уравнение вида
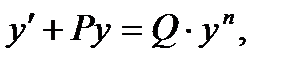 где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Г) Дифференциальное уравнение вида
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Г) Дифференциальное уравнение вида 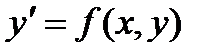 называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида 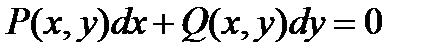 является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Д) Дифференциальное уравнение первого порядка вида: является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Д) Дифференциальное уравнение первого порядка вида:
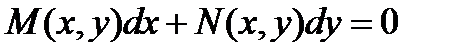 называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции 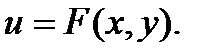
| |||||
4 Вопрос
Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
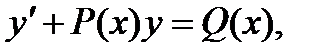 при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.
P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.
Линейные однородные дифференциальные уравнения.
Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.
P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.
Линейные однородные дифференциальные уравнения.
Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
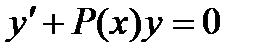 .
Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей. .
Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.
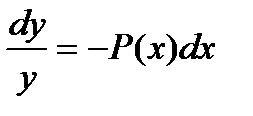 Линейные неоднородные дифференциальные уравнения.
Для интегрирования линейных неоднородных уравнений (Q(x)¹ 0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Метод Бернулли.
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций
Линейные неоднородные дифференциальные уравнения.
Для интегрирования линейных неоднородных уравнений (Q(x)¹ 0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Метод Бернулли.
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций 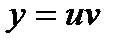 .
При этом очевидно, что .
При этом очевидно, что  - дифференцирование по частям.
Подставляя в исходное уравнение, получаем: - дифференцирование по частям.
Подставляя в исходное уравнение, получаем:
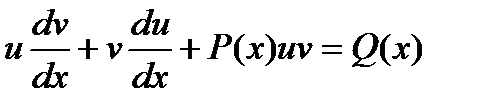
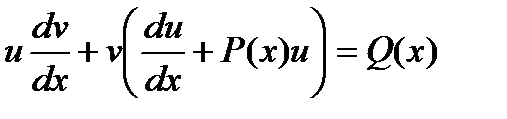 Далее следует важное замечание – т. к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение
Далее следует важное замечание – т. к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение 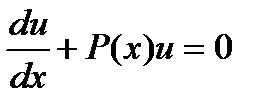 .
Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение .
Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение 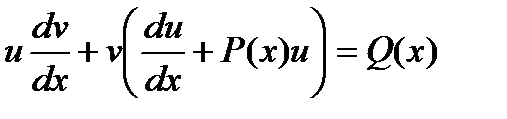 с учетом того, что выражение, стоящее в скобках, равно нулю.
Т. е. была получена вторая составляющая произведения с учетом того, что выражение, стоящее в скобках, равно нулю.
Т. е. была получена вторая составляющая произведения 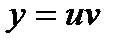 , которое и определяет искомую функцию. , которое и определяет искомую функцию.
|
5 Вопрос
Дифференциальное уравнение вида 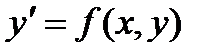 называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида 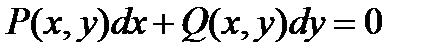 является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим однородное уравнение является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим однородное уравнение 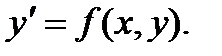 Т. к. функция f(x, y) – однородная нулевого измерения, то можно записать:
Т. к. функция f(x, y) – однородная нулевого измерения, то можно записать:
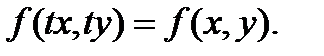 Т. к. параметр t вообще говоря произвольный, предположим, что
Т. к. параметр t вообще говоря произвольный, предположим, что  . Получаем: . Получаем:
 Правая часть полученного равенства зависит фактически только от одного аргумента
Правая часть полученного равенства зависит фактически только от одного аргумента 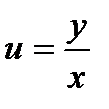 , т. е. , т. е.
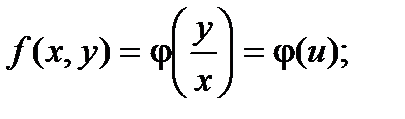 Исходное дифференциальное уравнение таким образом можно записать в виде:
Исходное дифференциальное уравнение таким образом можно записать в виде:
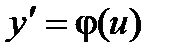 Далее заменяем y = ux,
Далее заменяем y = ux, 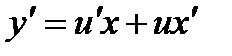 . .
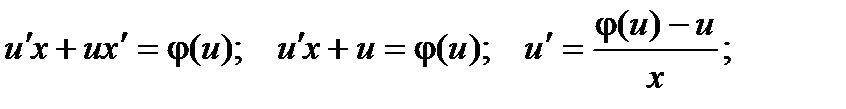 таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
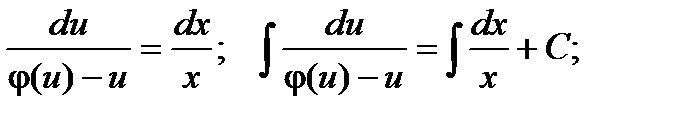 Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
| 6 Вопрос
Дифференциальное уравнение первого порядка вида:
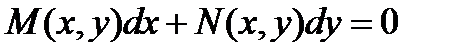 называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции 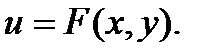 Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде:
Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде: 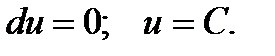 Таким образом, для решения надо определить:
1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;
2) как найти эту функцию.
Если дифференциальная форма
Таким образом, для решения надо определить:
1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;
2) как найти эту функцию.
Если дифференциальная форма
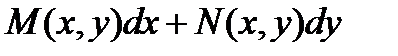 является полным дифференциалом некоторой функции u, то можно записать:
является полным дифференциалом некоторой функции u, то можно записать:
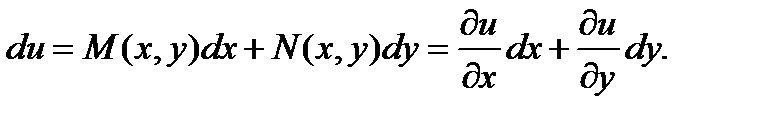 Т. е.
Т. е. 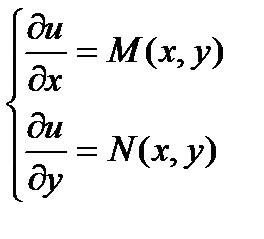 .
Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х: .
Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:
 Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.
Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.
 Теперь рассмотрим вопрос о нахождении собственно функции u.
Проинтегрируем равенство
Теперь рассмотрим вопрос о нахождении собственно функции u.
Проинтегрируем равенство 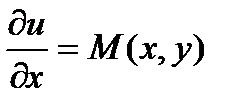 : :
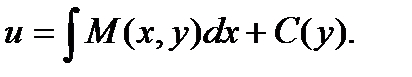 Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т. к. при интегрировании переменная у полагается постоянным параметром.
Определим функцию С(у).
Продифференцируем полученное равенство по у.
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т. к. при интегрировании переменная у полагается постоянным параметром.
Определим функцию С(у).
Продифференцируем полученное равенство по у.
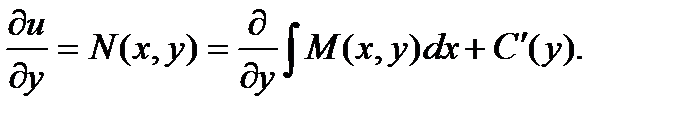 Откуда получаем:
Откуда получаем:
 Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.
Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.
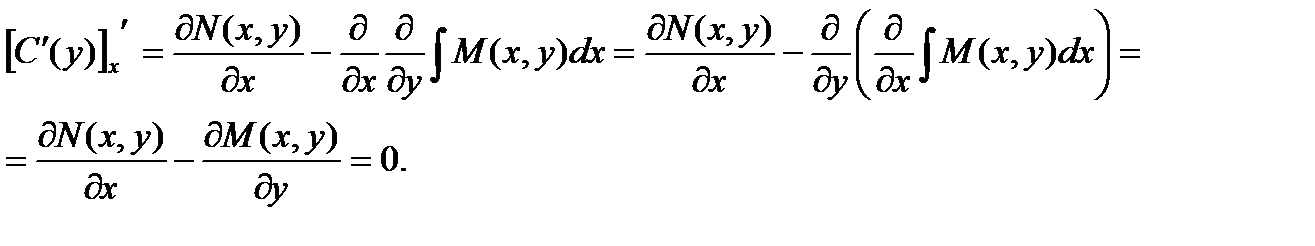 Теперь определяем функцию С(у):
Теперь определяем функцию С(у):
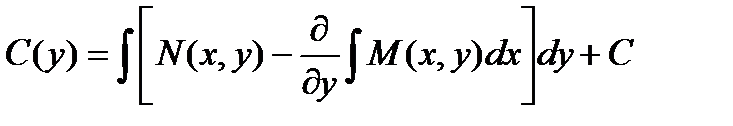 Подставляя этот результат в выражение для функции u, получаем:
Подставляя этот результат в выражение для функции u, получаем:
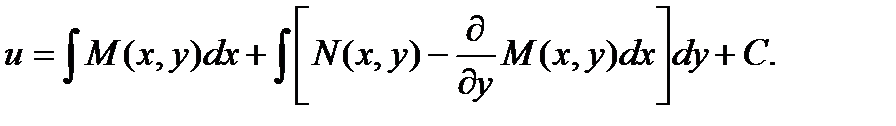 Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:
Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:
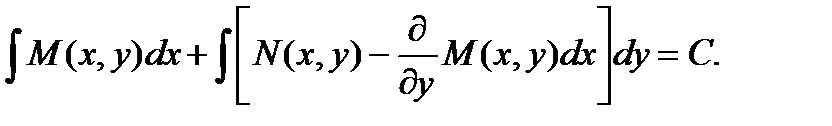
| |||||
7 Вопрос
Дифференциальным уравнением порядка n называется уравнение вида:
 В некоторых случаях это уравнение можно разрешить относительно y(n):
В некоторых случаях это уравнение можно разрешить относительно y(n):
 Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.
Решение
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.
Решение 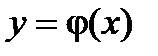 удовлетворяет начальным условиям удовлетворяет начальным условиям 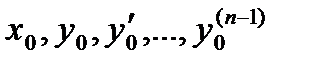 , если , если  Нахождение решения уравнения
Нахождение решения уравнения  , удовлетворяющего начальным условиям , удовлетворяющего начальным условиям 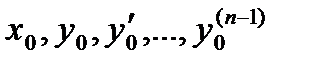 , называется решением задачи Коши.
Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).
Если функция (n-1) –й переменных вида , называется решением задачи Коши.
Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).
Если функция (n-1) –й переменных вида 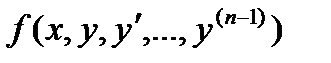 в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 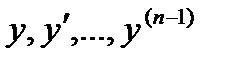 , то какова бы не была точка ( , то какова бы не была точка ( 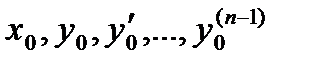 ) в этой области, существует единственное решение ) в этой области, существует единственное решение 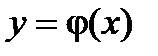 уравнения уравнения 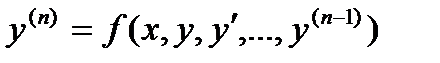 , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям 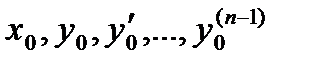
|
9 Вопрос
Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных  вида: вида:
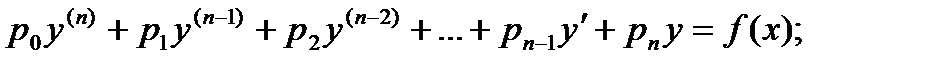 где p0, p1, …, pn – функции от х или постоянные величины, причем p0 ¹ 0.
Левую часть этого уравнения обозначим L(y).
где p0, p1, …, pn – функции от х или постоянные величины, причем p0 ¹ 0.
Левую часть этого уравнения обозначим L(y).
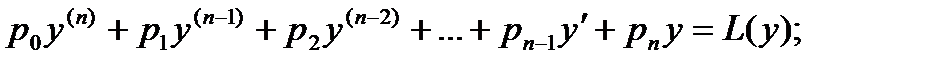 Если f(x) = 0, то уравнение L(y) = 0 называется линейным однороднымуравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p0, p1, p2, … pn – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.
Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких – либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение “близким” к нему линейным.
Рассмотрим способы интегрирования некоторых типов линейных дифференциальных уравнений высших порядков.
Линейные однородные дифференциальные уравнения с
произвольными коэффициентами.
Рассмотрим уравнение вида
Если f(x) = 0, то уравнение L(y) = 0 называется линейным однороднымуравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p0, p1, p2, … pn – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.
Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких – либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение “близким” к нему линейным.
Рассмотрим способы интегрирования некоторых типов линейных дифференциальных уравнений высших порядков.
Линейные однородные дифференциальные уравнения с
произвольными коэффициентами.
Рассмотрим уравнение вида 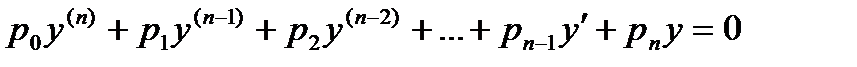 Выражение
Выражение 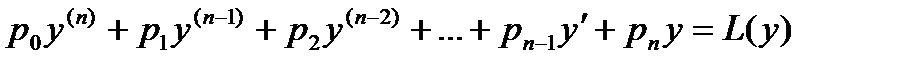 называется линейным дифференциальным оператором.
Линейный дифференциальный оператор обладает следующими свойствами:
1) называется линейным дифференциальным оператором.
Линейный дифференциальный оператор обладает следующими свойствами:
1) 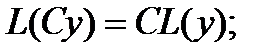 2)
2) 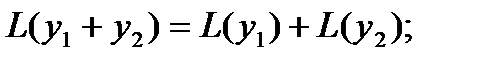 Решения линейного однородного уравнения обладают следующими свойствами:
1) Если функция у1 является решением уравнения, то функция Су1, где С – постоянное число, также является его решением.
2) Если функции у1 и у2 являются решениями уравнения, то у1 +у2 также является его решением.
Решения линейного однородного уравнения обладают следующими свойствами:
1) Если функция у1 является решением уравнения, то функция Су1, где С – постоянное число, также является его решением.
2) Если функции у1 и у2 являются решениями уравнения, то у1 +у2 также является его решением.
|
8 Вопрос
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y(n) = f(x).
Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

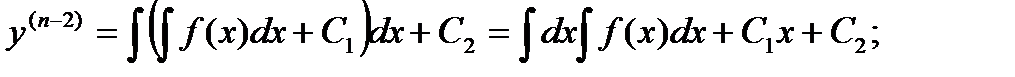 Уравнения, не содержащие явно искомой функции
и ее производных до порядка k – 1 включительно.
Это уравнения вида:
Уравнения, не содержащие явно искомой функции
и ее производных до порядка k – 1 включительно.
Это уравнения вида: 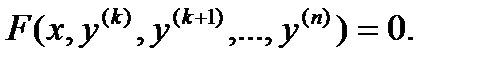 В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:
В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:
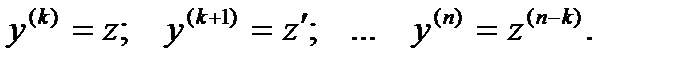 Тогда получаем:
Тогда получаем: 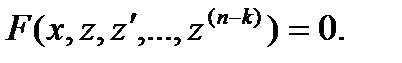 Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:
Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:
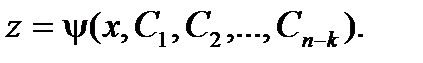 Делая обратную подстановку, имеем:
Делая обратную подстановку, имеем:
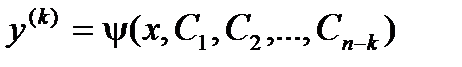 Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:
Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:
 Уравнения, не содержащие явно независимой переменной.
Это уравнения вида
Уравнения, не содержащие явно независимой переменной.
Это уравнения вида 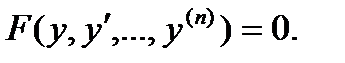 Порядок таких уравнений может быть понижен на единицу с помощью замены переменных
Порядок таких уравнений может быть понижен на единицу с помощью замены переменных 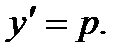
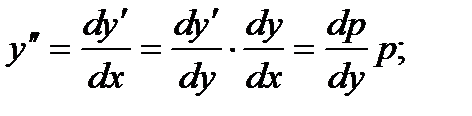
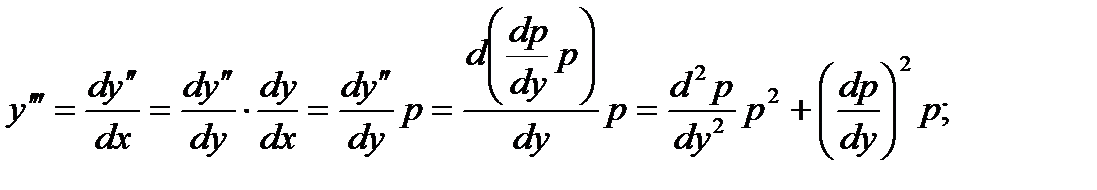 и т. д.
Подставляя эти значения в исходное дифференциальное уравнение, получаем: и т. д.
Подставляя эти значения в исходное дифференциальное уравнение, получаем:
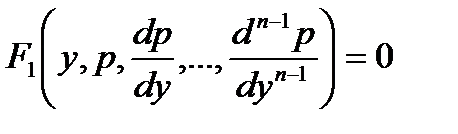 Если это уравнение проинтегрировать, и
Если это уравнение проинтегрировать, и 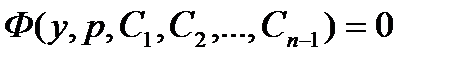 - совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка: - совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка:
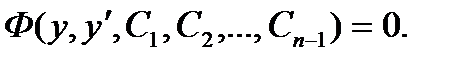
| |||||
| 10 Вопрос Структура общего решения. Фундаментальной системой решений линейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения. Если из функций yi составить определитель n – го порядка
то этот определитель называется определителем Вронского Теорема. Если функции Теорема. Если функции Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения Теорема. Если
1) Составляем характеристическое уравнение и находим его корни. 2) Находим частные решения дифференциального уравнения, причем: a) каждому действительному корню соответствует решение ekx; б) каждому действительному корню кратности m ставится в соответствие m решений: в) каждой паре комплексно – сопряженных корней
г) каждой паре m – кратных комплексно – сопряженных корней 3) Составляем линейную комбинацию найденных решений. | 11 Вопрос Лин неодн диф урав с пр к-ми. Рассмотрим уравнение вида С учетом обозначения
При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале ( конечном или бесконечном). Теорема. Общее решение линейного неоднородного дифференциального уравнения Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами Уравнения с правой частью специального вида. Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения. Различают следующие случаи: I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
где Тогда частное решение ищется в виде:
Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения. II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно. Тогда частное решение неоднородного уравнения будет иметь вид:
где число r показывает сколько раз число Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию. Т. е. если уравнение имеет вид:
Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами. | 12 Вопрос
Нормальные системы обыкновенных дифференциальных уравнений.
Совокупность соотношений вида:
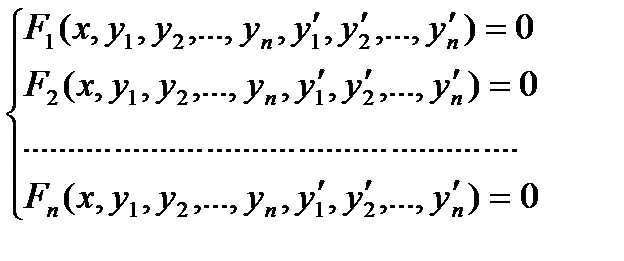 где х- независимая переменная, у1, у2, …, уn – искомые функции, называется системой дифференциальных уравнений первого порядка.
Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.
Такая система имеет вид:
где х- независимая переменная, у1, у2, …, уn – искомые функции, называется системой дифференциальных уравнений первого порядка.
Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.
Такая система имеет вид: 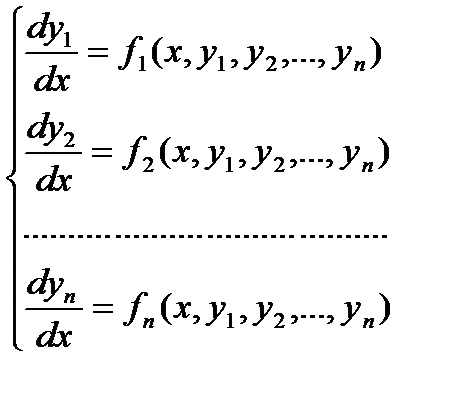 Общим решениемсистемы дифференциальных уравнений вида будет совокупность функций
Общим решениемсистемы дифференциальных уравнений вида будет совокупность функций 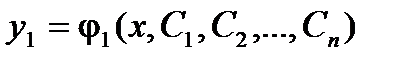 , , 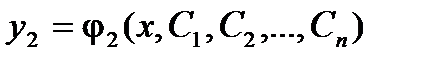 , … , … 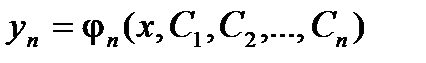 , которые при подстановке в систему обращают ее в тождество.
Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде: , которые при подстановке в систему обращают ее в тождество.
Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:
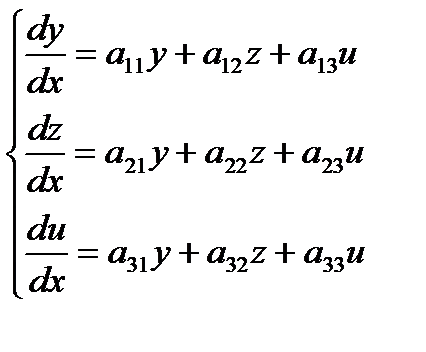
| |||||
6 вопрос
Признак Даламбера. Если предел отношения последующего члена ряда ( 1 ) к предыдущему меньше 1, то ряд сходится, если больше 1, то ряд расходится
Если 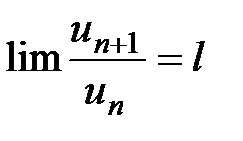 , то при l < 1 сход., при l > 1 расход., при l = 1 – сомнительный случай
Док-во. Отношения (un + 1 / un ) образуют вспомогательную числовую последовательность, которая может сходится или расходится. Необходимое условие сходимости: Для всякого e > 0 существует такое N, что при n > Nвыполняется неравенство l - e < un + 1 / un < l +e, т. е. с ростом n член последовательности оказывается в сколь угодно малой e - окрестности точки l.
Пусть l < 1, e мало и q = l +e < 1, тогда из условия uN + 1 / uN < qследует uN+1 < quN, uN+2 < q uN+1 < q2uN, uN+3 < q3uN, . . . В результате получаем две числовые последовательности: uN, uN+1, uN+2, . . . и uN, q uN, q2 uN, q3 uN. . . связанные неравенством uN+n < uN qn. Строим из них ряды. Т. к. ряд с большими членами (геометрическая прогрессия, q < 1) сходится, то ряд с меньшими членами , то при l < 1 сход., при l > 1 расход., при l = 1 – сомнительный случай
Док-во. Отношения (un + 1 / un ) образуют вспомогательную числовую последовательность, которая может сходится или расходится. Необходимое условие сходимости: Для всякого e > 0 существует такое N, что при n > Nвыполняется неравенство l - e < un + 1 / un < l +e, т. е. с ростом n член последовательности оказывается в сколь угодно малой e - окрестности точки l.
Пусть l < 1, e мало и q = l +e < 1, тогда из условия uN + 1 / uN < qследует uN+1 < quN, uN+2 < q uN+1 < q2uN, uN+3 < q3uN, . . . В результате получаем две числовые последовательности: uN, uN+1, uN+2, . . . и uN, q uN, q2 uN, q3 uN. . . связанные неравенством uN+n < uN qn. Строим из них ряды. Т. к. ряд с большими членами (геометрическая прогрессия, q < 1) сходится, то ряд с меньшими членами 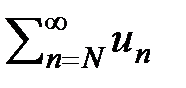 также сходится по признаку сравнения и по свойству 10 сходится исходный ряд также сходится по признаку сравнения и по свойству 10 сходится исходный ряд 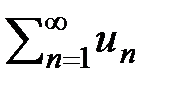 . При l > 1 аналогичным образом получаем обратный результат. . При l > 1 аналогичным образом получаем обратный результат.
| |||||||
| 13 Вопрос Метод Эйлера Известно, что уравнение Если взять последовательность точек х0, х1, х2, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию При подстановке заданных начальных условий (х0, у0) в дифференциальное уравнение
Заменив на отрезке [x0, x1] интегральную кривую на касательную к ней, получаем значение
Производя аналогичную операцию для отрезка [x1, x2], получаем:
Продолжая подобные действия далее, получаем ломаную кривую, которая называется ломаной Эйлера. Можно записать общую формулу вычислений:
Если последовательность точек хi выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:
Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета. Суть метода состоит в том, что в формуле
Затем находится значение производной в точке
Затем третье:
и т. д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М1 ломаной Эйлера. Аналогичная операция производится для остальных значений у. Подобное уточнение позволяет существенно повысить точность результата. | 1 вопрос
Числовым рядом наз. сумма членов бесконечной числовой последовательности
u1 + u2 + u3 +. . . + un +. . . = 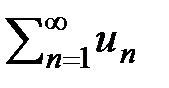 Непосредственно просуммировать ряд нельзя, т. к. число слагаемых бесконечно. Приходится вводить специальную процедуру.
Частичной суммой ряда Sn наз. сумма
ее первых n членов. Sn =
Непосредственно просуммировать ряд нельзя, т. к. число слагаемых бесконечно. Приходится вводить специальную процедуру.
Частичной суммой ряда Sn наз. сумма
ее первых n членов. Sn =  Частичные суммы ряда образуют вспомогательную числовую последовательность
S1, S2, S3, . . . , Sn, . . . , где Sn = Sn – 1 + un, которая может сходится или расходится.
Суммой числового ряда наз. предел последовательности частичных сумм ряда S = lim Sn при n ® ¥
Ряд наз. сходящимся, если предел конечен и расходящимся, если бесконечен.
Частичные суммы ряда образуют вспомогательную числовую последовательность
S1, S2, S3, . . . , Sn, . . . , где Sn = Sn – 1 + un, которая может сходится или расходится.
Суммой числового ряда наз. предел последовательности частичных сумм ряда S = lim Sn при n ® ¥
Ряд наз. сходящимся, если предел конечен и расходящимся, если бесконечен.
| 4 вопрос Гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных числам натурального ряда: т. е. сумма всех чисел вида 1/n, где n - натуральное число, изменяющееся от нуля до бесконечности. Ряд
очевидно, расходится, но и ряд
составленный из обратных величин соответствующих членов ряда (1), также расходится.
при неограниченном возрастании n стремится к неперову числу e как к своему пределу, всё время оставаясь меньше этого предела. Поэтому при любом положительном n имеем
Отсюда
или
или
Подставляя в последнее неравенство вместо n числа 1, 2, 3, 4, ..., получим неравенства: Складывая почленно эти неравенства, получим:
или Sn> ln(n+1)
а поэтому и
т. е. ряд (2) расходится.
| |||||
2 вопрос
Основные свойства сходящихся рядов.
10 Отбрасывание конечного числа членов не влияет на сходимость ряда.
Док-во. Имеем 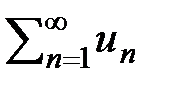 и и 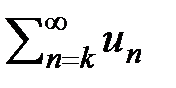 Пусть
Пусть 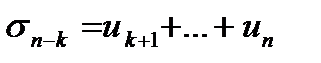 , тогда
lim Sn = lim(Sk + sn – k) = Sk + lim sn – k при n ® ¥
Если существует конечный предел слева, то существует предел и справа, т. е. укороченный ряд тоже сходится.
2. Если все члены ряда имеют общий
множитель, то он является общим множителем для всего ряда , тогда
lim Sn = lim(Sk + sn – k) = Sk + lim sn – k при n ® ¥
Если существует конечный предел слева, то существует предел и справа, т. е. укороченный ряд тоже сходится.
2. Если все члены ряда имеют общий
множитель, то он является общим множителем для всего ряда  = с = с  = с S. Это свойство пределов.
30 Почленное сложение двух рядов приводит к сложению их сумм. (Это свойство пределов) = с S. Это свойство пределов.
30 Почленное сложение двух рядов приводит к сложению их сумм. (Это свойство пределов) 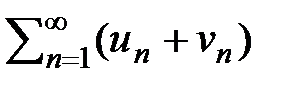 = = 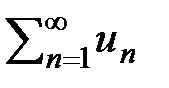 + + 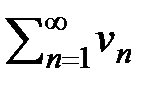 = S1 + S2 = S1 + S2
| |||||||
3 вопрос
| |||||||
| 5 вопрос (Признак сравнения) Пусть даны два знакоположительных числовых ряда причём un≤ vn при любых n=1, 2, …. Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7); 2. Если ряд (7) расходится, то расходится и ряд (8). Доказательство. Обозначим n-е частичные суммы рядов (7) и (8) через Sn и sn соответственно. Пусть ряд (8) сходится. Это значит, что существует конечный Замечания. 1. В силу теоремы 1 признак сравнения справедлив и в случае, если un≤ vn начиная с некоторого номера к, то есть при n≥ k. 2. Для использования признака сравнения нужно иметь для сравнения ряды, про которые заранее известно, сходятся они или расходятся. В качестве таких рядов можно использовать сходящуюся бесконечно убывающую геометрическую прогрессию, а также обобщённые гармонические ряды Пример Исследовать на сходимость ряд Рассмотрим расходящийся ряд Он расходится, так как получен из гармонического ряда отбрасыванием u1=1. Так как ln(n+1)< n+1 при любом n=1, 2, …, то (Предельный признак сравнения) Пусть даны два знакоположительных числовых ряда (7) и (8). Если существует конечный предел Доказательство. По условию теоремы существует конечный предел Неравенство (9) верно при любом E> 0. Выберем поэтому Е так, чтобы выполнялось А-Е> 0. Если ряд (8) сходится, то сходится и ряд Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда. Пример. Исследовать на сходимость ряд Возьмём для сравнения ряд с общим членом vn= следовательно, данный ряд расходится по предельному признаку сравнения.
13 вопрос Свойства равномерно сходящихся рядов. 1) Теорема о непрерывности суммы ряда. Если члены ряда 2)Теорема о почленном интегрировании ряда. Равномерно сходящийся на отрезке [a, b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т. е. ряд, составленный из интегралов от его членов по отрезку [a, b], сходится к интегралу от суммы ряда по этому отрезку.
3) Теорема о почленном дифференцировании ряда. Если члены ряда
|
7 вопрос (Признак Коши) Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7) и пусть существует предел Доказательство. По условию существует p-E< Пусть p< 1. Выберем Е таким, чтобы выполнялось p+E=q< 1. Тогда из (14) получаем Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un< qn для всех n³ N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7). Пусть теперь p> 1. Выберем Е так, чтобы выполнялось условие
9 вопрос Знакочередующимся наз. числовой ряд вида Признак Лейбница. Если члены ряда ( 3 ) последовательно убывают (un > un+1 )и стремятся к 0 ( lim un = 0 при n ® ¥ ), то ряд сходится, причем, его сумма S > 0иS < u1. Док-во. Члены частичной суммы S2m сгруппируем двумя способами: S2m = (u1 – u2) + (u3 – u4) +. . . +(u2m-1 – u2m) ( a ) S2m = u1 – (u2 – u3) – (u4 – u5) -. . . – (u2m-2 – u2m-1) – u2m ( b ) При способе ( а ) имеем сумму положительных членов S2m > 0. При способе (b) имеем разность между u1 и суммой (m – 1) положительногослагаемого. Из этого следует, что S2m всегда ограничена S2m < u1, а последовательность ограниченных S2m имеет предел, т. е. ряд сходится. От S2m+1 легко перейти к S2m, выделив лишний член.
10 вопрос Знакопеременным наз. числовой ряд составленный из положительных и отрицательных членов. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости) Пусть u1+u2+…+un+…= знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов │ u1│ +│ u2│ +…+│ un │ +…= Тогда ряд (20) тоже сходится. Доказательство. Рассмотрим вспомогательный ряд (u1+│ u1│ )+(u2+│ u2│ )+…+(un+│ un│ )+…= Очевидно, 0≤ un+│ un│ ≤ 2│ un│ при всех n=1, 2, …. Ряд (21) сходится по условию, поэтому сходится ряд Замечание. Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться. Например, ряд Абсолютная и условная сходимость рядов. Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков). и ряд, составленный из абсолютных величин членов ряда (1): Теорема. Из сходимости ряда (2) следует сходимость ряда (1). Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого e> 0 существует число N, такое, что при n> N и любом целом p> 0 верно неравенство:
По свойству абсолютных величин:
То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1). Ряд Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают. Ряд
|
8 вопрос
(Интегральный признак Коши)
Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1³ u2≥ …≥ un≥ … и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1; ∞ ) функция, что f(1)=u1, f(2)=u2, …, f(n)= =un, …. Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом 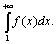
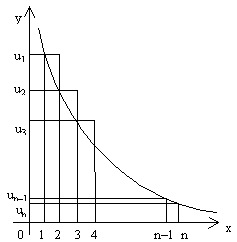 Доказательство. Построим график функции y=f(x) на отрезке [1; n] и построим прямоугольник с основаниями [1; 2], [2; 3], …, [n-1; n] и высотами u1, u2, …, un-1, а также с высотами u2, u3, …, un.
Sn=u1+u2+…+un-1+un, Sвпис=u2. 1+u3. 1+…+un. 1=u2+u3+…+un=Sn-u1,
Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь криволинейной трапеции S=
Доказательство. Построим график функции y=f(x) на отрезке [1; n] и построим прямоугольник с основаниями [1; 2], [2; 3], …, [n-1; n] и высотами u1, u2, …, un-1, а также с высотами u2, u3, …, un.
Sn=u1+u2+…+un-1+un, Sвпис=u2. 1+u3. 1+…+un. 1=u2+u3+…+un=Sn-u1,
Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь криволинейной трапеции S= 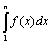 Получаем Sn-u1<
Получаем Sn-u1< 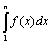 < Sn-un.
Отсюда
Sn< u1+ < Sn-un.
Отсюда
Sn< u1+ 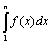 (17)
и Sn> un+ (17)
и Sn> un+ 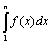 (18)
Пусть (18)
Пусть 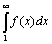 сходится. Это означает, что существует конечный предел сходится. Это означает, что существует конечный предел  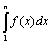 =Y. Соотношение (17) принимает вид: Sn< u1+Y при любом n. Это означает, что последовательность частичных сумм Sn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть =Y. Соотношение (17) принимает вид: Sn< u1+Y при любом n. Это означает, что последовательность частичных сумм Sn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть 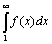 расходится. Это означает, что расходится. Это означает, что  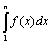 =∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.
Пример.
Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд =∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.
Пример.
Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд 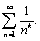 Очевидно, f(x)=
Очевидно, f(x)=  .
При к≠ 1 имеем .
При к≠ 1 имеем 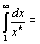 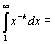  = = 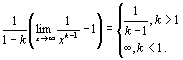 При к=1 имеем При к=1 имеем 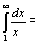 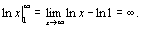 Таким образом, обобщённый гармонический ряд сходится при k> 1 и расходится при k≤ 1.
Таким образом, обобщённый гармонический ряд сходится при k> 1 и расходится при k≤ 1.
| |||||
| 11 вопрос Функциональным наз. ряд члены которого являются функциями от х. При фиксированном x = a функциональный ряд становится числовым. Частными (частичными) суммами функционального ряда Функциональный ряд Совокупность всех значений х, для которых сходится ряд Ряд Теорема. (Критерий Коши равномерной сходимости ряда) Для равномерной сходимости ряда выполнялось бы для всех х на отрезке [a, b]. 12 вопрос Признак Вейерштрасса равномерной сходимости функционального ряда.
Теорема. Если для функционального ряда Д-во: По усл-ю (2) для любого n Из (3) и (4) следует, что для ряда (1) вып. Усл-е Коши на мн-ве Е, в силу этого по критерию Коши — ряд сх-ся равномерно на мн-ве Е. Абсолютная сх-ть ряда для каждого Следствие: Если сх-ся ряд
| |||||||
15 вопрос
(теорема Абеля). Если степенной ряд (1. 2) сходится при некотором 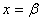 , где , где 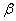 -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что 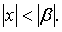 Наоборот, если ряд (12) расходится при Наоборот, если ряд (12) расходится при 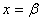 , то он расходится при всех значениях x таких, что , то он расходится при всех значениях x таких, что 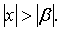 Доказательство. Пусть числовой ряд
Доказательство. Пусть числовой ряд 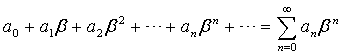 (1. 3)
сходится. Поэтому (1. 3)
сходится. Поэтому 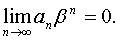 Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что  для всех n=0, 1, 2, …
Рассмотрим теперь ряд для всех n=0, 1, 2, …
Рассмотрим теперь ряд
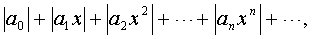 (1. 4)
предполагая, что (1. 4)
предполагая, что  Так как Так как 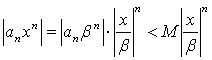 и при этом и при этом 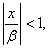 то члены ряда (3. 4) не превосходят соответствующих членов сходящегося ряда то члены ряда (3. 4) не превосходят соответствующих членов сходящегося ряда
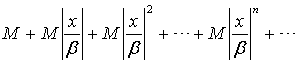 (геометрической прогрессии). Следовательно, ряд (1. 4) сходится, а ряд (1. 2) абсолютно сходится.
Предположим теперь, что ряд (1. 3) расходится, а ряд (1. 2) сходится при
(геометрической прогрессии). Следовательно, ряд (1. 4) сходится, а ряд (1. 2) абсолютно сходится.
Предположим теперь, что ряд (1. 3) расходится, а ряд (1. 2) сходится при 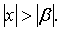 Но тогда из сходимости ряда (1. 2) следует сходимость и ряда (1. 3), что противоречит предположению. Теорема доказана.
Теорема Абеля позволяет дать описание области сходимости степенного ряда.
Теорема 1. 2. Для степенного ряда (1. 2) возможны только три случая:
1) ряд сходится в единственной точке x=0;
2) ряд сходится при всех значениях x;
3) существует такое R> 0, что ряд сходится при всех значениях x, для которых Но тогда из сходимости ряда (1. 2) следует сходимость и ряда (1. 3), что противоречит предположению. Теорема доказана.
Теорема Абеля позволяет дать описание области сходимости степенного ряда.
Теорема 1. 2. Для степенного ряда (1. 2) возможны только три случая:
1) ряд сходится в единственной точке x=0;
2) ряд сходится при всех значениях x;
3) существует такое R> 0, что ряд сходится при всех значениях x, для которых 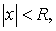 и расходится при всех x, для которых и расходится при всех x, для которых 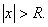
|
16 вопрос
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
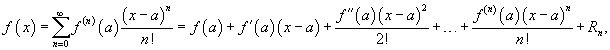 где Rn − остаточный член в форме Лагранжа определяется выражением
где Rn − остаточный член в форме Лагранжа определяется выражением
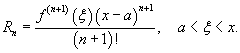 Если приведенное разложение сходится в некотором интервале x, т. е.
Если приведенное разложение сходится в некотором интервале x, т. е. 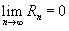 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена: , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена:
 Имеем степенной ряд, сходящийся на интервале (x0 – R, x0 + R). Суммой ряда является функция f(x)
Имеем степенной ряд, сходящийся на интервале (x0 – R, x0 + R). Суммой ряда является функция f(x)
 =f(x) ( 11 )
Покажем, что коэффициенты этого ряда связаны простым соотношением с f(x).
Будем последовательно дифференцировать обе части равенства ( 11 ) и вычислять производные при х = х0
f (x) = a0 + a1(x – x0) + a2(x – x0)2 + a3(x – x0)3 + … + an(x – x0)n +. . . , f(x0) = a 0
f ‘(x) = a1 + a2(x – x0) + a3(x – x0)2 + … + n an(x – x0)n-1 +. . . , f ‘(x0) = a1
f ‘’(x) = a2 + a3(x – x0) + a4(x – x0)2 + … + n(n – 1) an(x – x0)n-2 +. . . , f ‘)’(x0) = 2 a2
f ‘’’(x) = a3 + a4(x – x0) + a5(x – x0)2 +…+ n(n–1)(n–2)an(x – x0)n-3 +. . . , f’’’(x0) = 23 a3
f(n) (x) = n(n–1)(n–2). . . 2 1 an +. . . , f ( n )(x0) = n! a n
Отсюда находим коэффициенты a0 = f(x0), an = f ( n )(x0) / n! ( 12 )
Таким образом, если бесконечно дифференцируемая в точке х0 функция f(x)разлагается в степенной ряд, то этот ряд имеет вид
f(x)= =f(x) ( 11 )
Покажем, что коэффициенты этого ряда связаны простым соотношением с f(x).
Будем последовательно дифференцировать обе части равенства ( 11 ) и вычислять производные при х = х0
f (x) = a0 + a1(x – x0) + a2(x – x0)2 + a3(x – x0)3 + … + an(x – x0)n +. . . , f(x0) = a 0
f ‘(x) = a1 + a2(x – x0) + a3(x – x0)2 + … + n an(x – x0)n-1 +. . . , f ‘(x0) = a1
f ‘’(x) = a2 + a3(x – x0) + a4(x – x0)2 + … + n(n – 1) an(x – x0)n-2 +. . . , f ‘)’(x0) = 2 a2
f ‘’’(x) = a3 + a4(x – x0) + a5(x – x0)2 +…+ n(n–1)(n–2)an(x – x0)n-3 +. . . , f’’’(x0) = 23 a3
f(n) (x) = n(n–1)(n–2). . . 2 1 an +. . . , f ( n )(x0) = n! a n
Отсюда находим коэффициенты a0 = f(x0), an = f ( n )(x0) / n! ( 12 )
Таким образом, если бесконечно дифференцируемая в точке х0 функция f(x)разлагается в степенной ряд, то этот ряд имеет вид
f(x)=  ( 13 )
и наз. рядом Тейлора, а при х0 = 0 наз. рядом Маклорена ( 13 )
и наз. рядом Тейлора, а при х0 = 0 наз. рядом Маклорена
|
14 вопрос
Степенным рядомназывается ряд вида
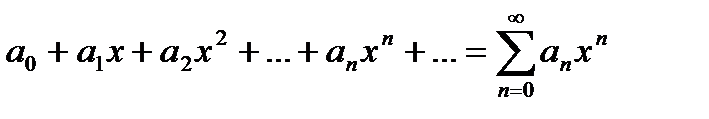 Интервал и радиус сходимости
Рассмотрим функцию
Интервал и радиус сходимости
Рассмотрим функцию  . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. Если интервал сходимости представляется в виде . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. Если интервал сходимости представляется в виде 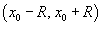 , где R > 0, то величина R называетсярадиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле , где R > 0, то величина R называетсярадиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
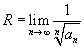 или на основе признака Даламбера:
или на основе признака Даламбера:
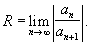
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
 ,
, 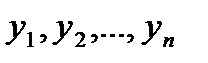 линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю. 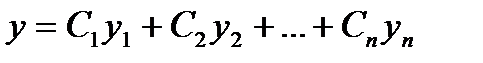 , где Ci –постоянные коэффициенты.
, где Ci –постоянные коэффициенты. 
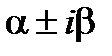 характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения: 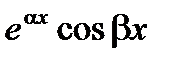 и
и 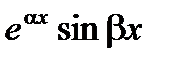 .
. 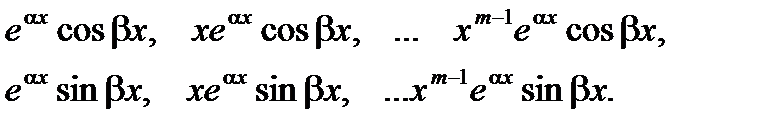
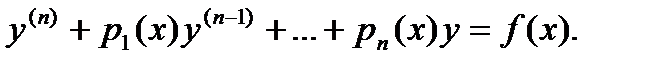
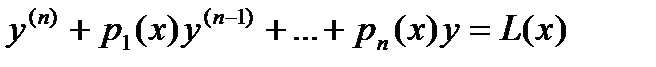 можно записать:
можно записать: 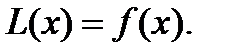
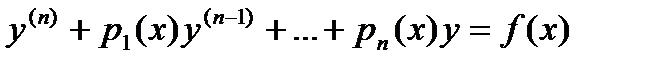 в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.
в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения. 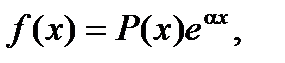
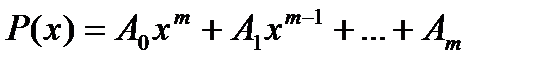 - многочлен степени m.
- многочлен степени m. 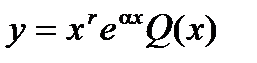

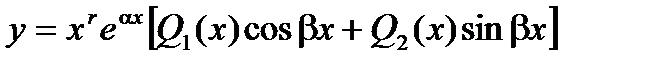
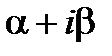 является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.
является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2. 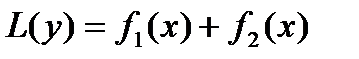 , то частное решение этого уравнения будет
, то частное решение этого уравнения будет 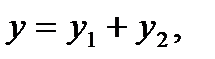 где у1 и у2 – частные решения вспомогательных уравнений
где у1 и у2 – частные решения вспомогательных уравнений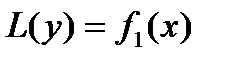 и
и 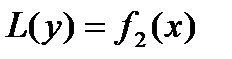
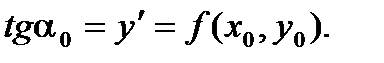
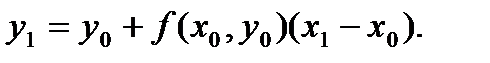
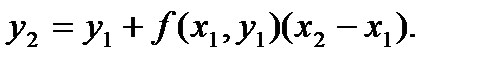
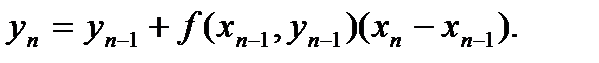
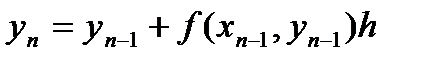
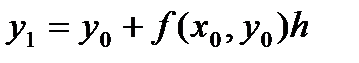 вместо значения
вместо значения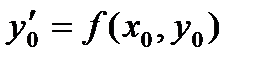 берется среднее арифметическое значений f(x0, y0) и f(x1, y1). Тогда уточненное значение:
берется среднее арифметическое значений f(x0, y0) и f(x1, y1). Тогда уточненное значение: 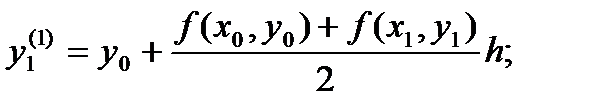
 . Заменяя f(x0, y0) средним арифметическим значений f(x0, y0) и
. Заменяя f(x0, y0) средним арифметическим значений f(x0, y0) и  , находят второе уточненное значение у1.
, находят второе уточненное значение у1. 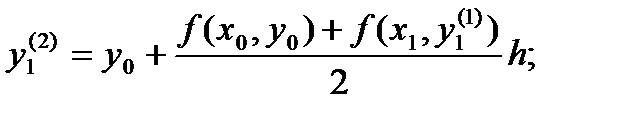
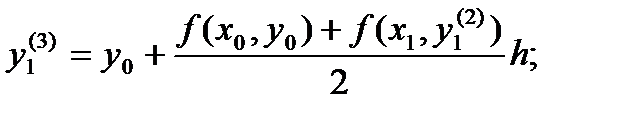
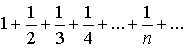

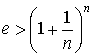 .
. 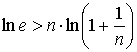 ,
, 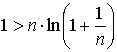 ,
, 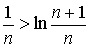 .
. 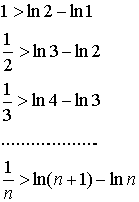
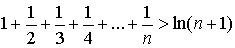 ,
, 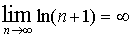 ,
, 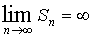 ,
, 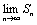 =S. Тогда имеет место также равенство
=S. Тогда имеет место также равенство 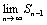 =S, так как при n
=S, так как при n  и (n-1)
и (n-1)  -
- 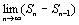 =
= 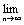 un≠ 0, то ряд u1+u2+…+un… расходится.
Пример.
Ряд
un≠ 0, то ряд u1+u2+…+un… расходится.
Пример.
Ряд  расходится, так как
расходится, так как
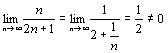 .
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что
.
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что 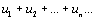 (7)
(7)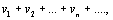 (8)
(8) =s. По условию теоремы 0< un≤ vn, поэтомуSn< sn< s при всех n=1, 2, …, то есть последовательность {Sn} ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть
=s. По условию теоремы 0< un≤ vn, поэтомуSn< sn< s при всех n=1, 2, …, то есть последовательность {Sn} ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть 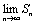 =∞ . Тогда из неравенства Sn< sn следует, что и
=∞ . Тогда из неравенства Sn< sn следует, что и  =∞ , следовательно, ряд (8) расходится. Теорема доказана.
=∞ , следовательно, ряд (8) расходится. Теорема доказана. 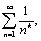 где к – действительное число. Несколько позже будет доказано, что при к≤ 1 такие ряды расходятся, а при k> 1 сходятся. При к=1 получаем уже упоминавшийся расходящийся гармонический ряд.
где к – действительное число. Несколько позже будет доказано, что при к≤ 1 такие ряды расходятся, а при k> 1 сходятся. При к=1 получаем уже упоминавшийся расходящийся гармонический ряд. 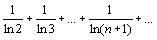 .
. 
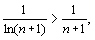 поэтому данный ряд расходится по признаку сравнения.
поэтому данный ряд расходится по признаку сравнения. 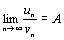 ≠ 0, то ряды (7) и (8) сходятся или расходятся одновременно.
≠ 0, то ряды (7) и (8) сходятся или расходятся одновременно. 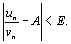 Последнее неравенство равносильно двойному неравенству –E<
Последнее неравенство равносильно двойному неравенству –E< 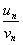 -A< E или A-E<
-A< E или A-E< 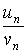 < A+E или
< A+E или 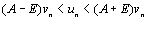 (9)
(9)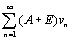 по теореме 2. Но тогда по признаку сравнения, учитывая (9), сходится и ряд (7). Если ряд (7) сходится, то по признаку сравнения, учитывая (9), сходится ряд
по теореме 2. Но тогда по признаку сравнения, учитывая (9), сходится и ряд (7). Если ряд (7) сходится, то по признаку сравнения, учитывая (9), сходится ряд 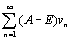 и по теореме 2 сходится ряд (8). Аналогично доказывается, учитывая (9), что из расходимости одного из рядов следует расходимость другого ряда. Докажите эту часть самостоятельно.
и по теореме 2 сходится ряд (8). Аналогично доказывается, учитывая (9), что из расходимости одного из рядов следует расходимость другого ряда. Докажите эту часть самостоятельно. 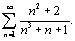 Здесь un=
Здесь un= 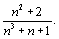
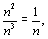 то есть расходящийся гармонический ряд
то есть расходящийся гармонический ряд 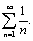 Применим предельный признак сравнения.
Применим предельный признак сравнения. 
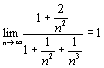 ¹ 0,
¹ 0, 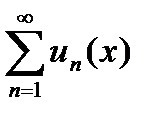 - непрерывные на отрезке [a, b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a, b].
- непрерывные на отрезке [a, b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a, b]. 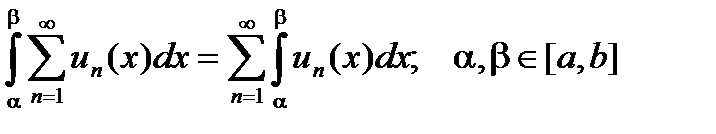
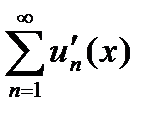 сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно. 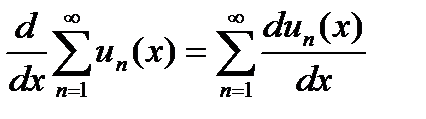
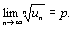 При p< 1 ряд (7) сходится, при p> 1 ряд (7) расходится.
При p< 1 ряд (7) сходится, при p> 1 ряд (7) расходится. 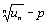 | < E или
| < E или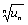 < p+E. (14)
< p+E. (14)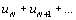 (15)
(15)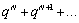 (16)
(16)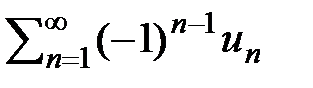 , un > 0 ( 3 )
, un > 0 ( 3 )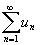 (20)
(20) │ un │. (21)
│ un │. (21)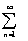 (un+│ un│ ). (22)
(un+│ un│ ). (22)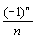 сходится по признаку Лейбница, а ряд
сходится по признаку Лейбница, а ряд  расходится (это гармонический ряд).
расходится (это гармонический ряд). 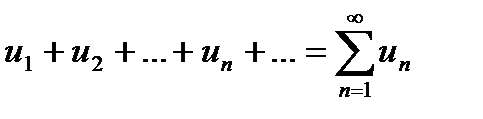 (1)
(1)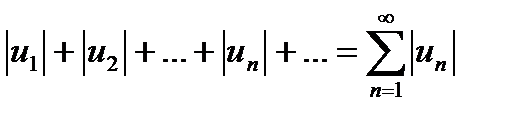 (2)
(2)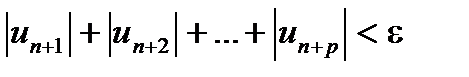
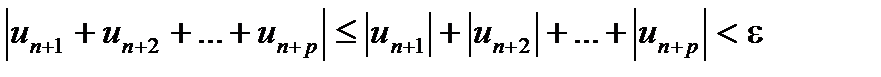

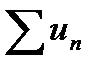 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 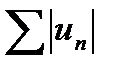 .
. 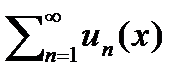 = u1(x) + u2(x) + u3(x) +. . . = S(x) ( 4 )
= u1(x) + u2(x) + u3(x) +. . . = S(x) ( 4 )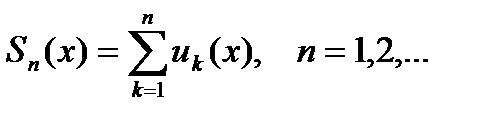
 называется суммой ряда
называется суммой ряда 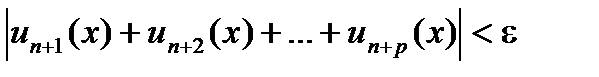
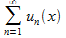 (1) можно указать такой сходящийся числовой ряд
(1) можно указать такой сходящийся числовой ряд  , что для всех n
, что для всех n  и для всех
и для всех 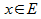 вып-ся усл-е
вып-ся усл-е  (2), то ряд (1) сх-ся абсолютно и равномерно на мн-ве Е.
(2), то ряд (1) сх-ся абсолютно и равномерно на мн-ве Е. 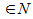 и для каждого
и для каждого 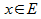 вы-ся нер-во:
вы-ся нер-во: 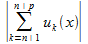
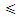
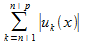
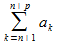 (3). Из сх-ти ряда
(3). Из сх-ти ряда 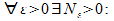
 n
n 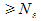

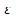 (4).
(4). 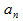 =sup
=sup 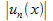 ,
,