Площадь криволинейной трапеции. Интеграл и его свойства.

Повторить тему вычисление первообразных, записать в тетрадь таблицу интегралов

1)изучить конспект урока, выполнить тренировочные задания 2)выполнить контрольные задания и отправить на проверку 3)выполнить задания в печатной тетради (ответы на вопросы )

Площадь криволинейной трапеции. Интеграл и его свойства.

Перечень вопросов, рассматриваемых в теме

1) Нахождение определенного интеграла

2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница

3) Решение задач, с помощью формулы Ньютона – Лейбница

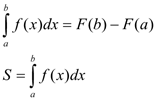
Формула Ньютона – Лейбница

Основная литература:

Колягин Ю. М., Ткачева М. В, Федорова Н. Е. и др., под ред. Жижченко А. Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА. Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

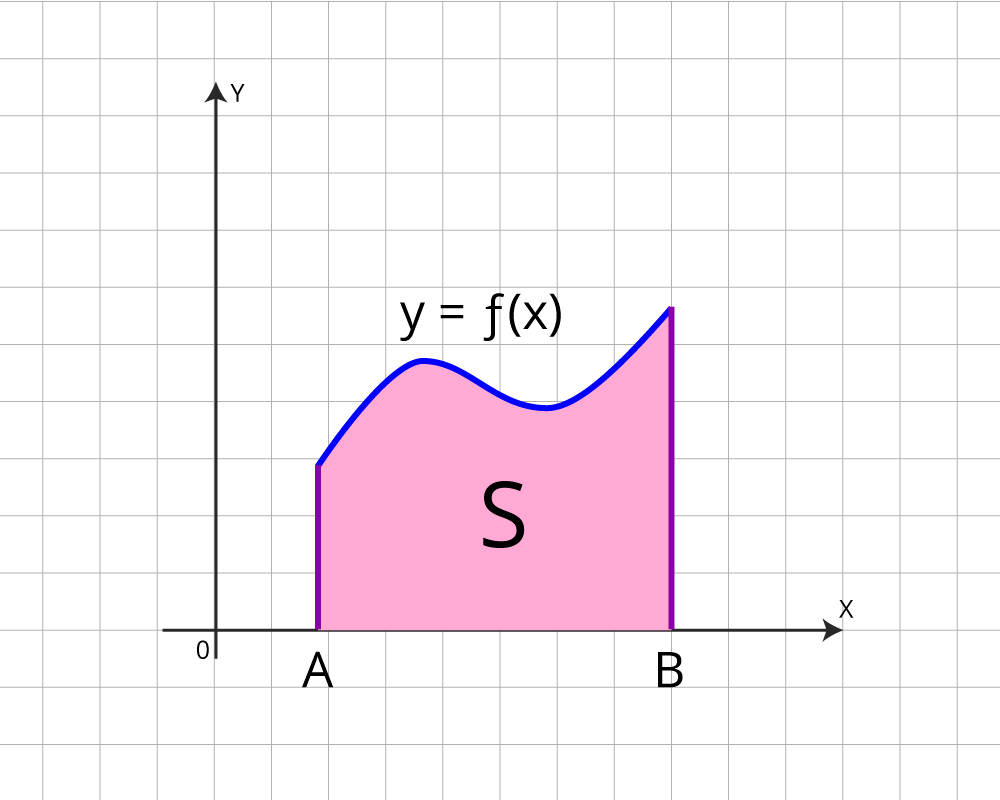
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а; b] знака функции f(х), прямыми х=а, x=b и отрезком [а; b].

Отрезок [a; b ] называют основанием этой криволинейной трапеции

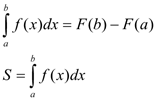
формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).

12 Следующая ⇒