Тема 1. «Понятие производной». Задание №1.Изучите тему в учебнике на стр. 171-172 Занятие 3. Понятие производной.(п.1) Не конспектируем!!!. Задание №2. Пройдите по ссылке и посмотрите видео Понятие производной https://www.youtube.com/watch?tim

Тема 1. «Понятие производной»

Задание №1. Изучите тему в учебнике на стр. 171-172 Занятие 3. Понятие производной. (п. 1) Не конспектируем!!!

Задание №2. Пройдите по ссылке и посмотрите видео " Понятие производной" https: //www. youtube. com/watch? time_continue=13& v=QygmvlwtyXQ& feature=emb_logo

Задание №3. Запишите в тетрадь конспект " Геометрический и физический смысл производной"

Тема 2. Геометрический и механический смысл производной

Прямая задается уравнением y =kx +b. Коэффициент k и является угловым коэффициентом этой прямой.

Геометрический смысл производной заключается в том, что угловой коэффициент касательной равен тангенсу острого угла, образуемого этой прямой с осью абсцисс и значению производной в точке касания.

k= tg α =f′ (x_о)

Здесь угол α – это угол между прямойy =kx +bи положительным направлением оси абсцисс. Он называетсяуглом наклона прямой.

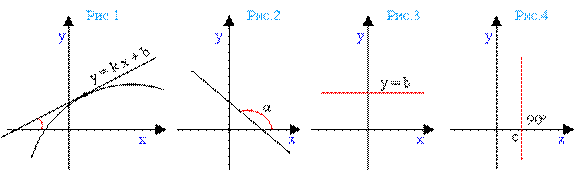
Если угол наклона прямойy =kx +bострый, то угловой коэффициент является положительным числом. График возрастает (рис. 1).

Если угол наклона прямойy =kx +bтупой, то угловой коэффициент является отрицательным числом. График убывает (рис. 2).

Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис. 3).

Если угол наклона прямой равен 90º (π /2), то прямая перпендикулярна оси абсцисс, то прямая задается равенством x =c, где c – некоторое действительное число (рис. 4).