Лекция. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. 1. Понятие первообразной функции и неопределенного интеграла

Лекция

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1. Понятие первообразной функции и неопределенного интеграла

Во многих вопросах науки и техники приходится по известной производной восстанавливать саму функцию. Например, используя ленту скоростемера, мы находим функцию 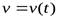скорости поезда в зависимости от времени. Но если мы хотим узнать, на каком километре пути находился поезд в тот или иной момент времени, нам нужно найти функцию 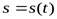зависимости пройденного пути от времени. Как известно, производной функции 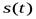будет функция 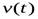, поэтому наша задача свелась к нахождению по заданной функции 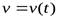неизвестной функции 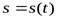, для которой производной будет .

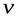Определение. Функция 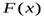в данном промежутке 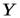называется первообразной функцией для функции 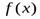, если на всем промежутке 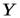функция 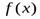является производной для функции 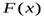, т. е. 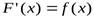или, что то же самое, 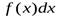служит для 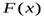дифференциалом, т. е. .

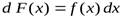Теорема. Если в некотором (конечном или бесконечном) промежутке 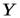функция 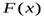есть первообразная для 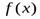, то и функция 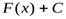, где 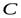- любая постоянная, также будет первообразной. Обратно, каждая функция, первообразная для 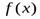в промежутке 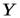, может быть представлена в этой форме.

В силу этой теоремы выражени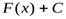е , где 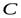- произвольная постоянная, представляет собой общий вид функции, которая имеет производную 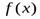. Это выражение называется неопределенным интегралом и обозначается 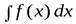. Произведение 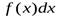называется подынтегральным выражением, а функция 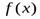- подынтегральной функцией.

12 Следующая ⇒