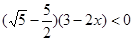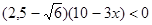- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение линейных неравенств с одной переменной
Решение линейных неравенств с одной переменной
|
Теория |
Практика | ||
Простейшее линейное неравенство вида 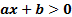 Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, но равносильным данному. Такие замены осуществляются на основе следующих утверждений:
1 Если какой-либо член неравенства с переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство равносильное данному.
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, но равносильным данному. Такие замены осуществляются на основе следующих утверждений:
1 Если какой-либо член неравенства с переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство равносильное данному.
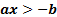 2 a) Если обе части неравенства с переменной умножить или разделить на одно и тоже положительное число, оставив при этом без изменения знак неравенства, то получится неравенство равносильное данному.
2 a) Если обе части неравенства с переменной умножить или разделить на одно и тоже положительное число, оставив при этом без изменения знак неравенства, то получится неравенство равносильное данному.
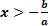 , , 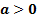 b) Если обе части неравенства с переменной умножить или разделить на одно и тоже отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство равносильное данному.
b) Если обе части неравенства с переменной умножить или разделить на одно и тоже отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство равносильное данному.
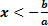 , , 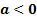
| 1 Решить неравенство: Решение. Согласно утверждению 1, получим: Ответ: 2. Решите неравенство Решение. Умножим обе части неравенства Ответ: -5. 3*. Решите неравенство Решение: 1) Определим знак разности Реши сам: 1. Решите неравенство 1) 2. Решите неравенство 1) 3. Решите неравенство 1) 4 Решите неравенство 1) 5* Решите неравенство 6* Решите неравенство 7* Решите неравенство | ||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
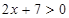 .
. 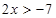 . По утверждению 2:
. По утверждению 2: 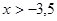 . Промежуток
. Промежуток 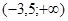 будет являться решением неравенства.
будет являться решением неравенства. 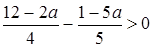
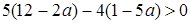 .
. 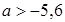 .
. 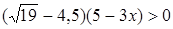 .
. 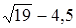 .
. 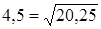 и
и 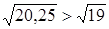 , то
, то 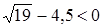 .
. 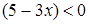 . Отсюда
. Отсюда 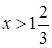 .
. 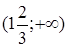 .
. 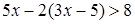
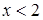 2)
2) 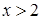 3)
3) 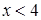 4)
4) 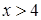
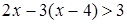
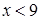 2)
2) 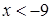 3)
3) 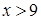 4)
4) 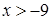
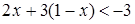
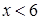 2)
2) 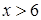 3)
3) 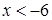 4)
4) 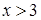
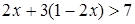
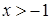 2)
2) 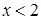 3)
3) 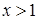 4)
4) 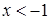
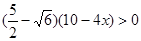 .
.