
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Геометрии 11 класс Уроки 1 -2. Теорию просто читаем
21. 05. 2020. И-106 Математика.
Раздел: Метод координат в пространстве.
Тема: Координаты вектора в пространстве
1. На ресурсе (Российская электронная школа) знакомимся с теорией по теме пройдя по ссылке: https: //resh. edu. ru/subject/17/11/
Геометрии 11 класс Уроки 1 -2. Теорию просто читаем
2. Дальше отрабатываем новый материал в рабочей тетради.
3. Задание по теме выполняем в своих тетрадях или на листах А4; фотографируем, присылаем. (На почту или в ВК)
Рабочая тетрадь по теме Метод координат: Координаты вектора.
1. Метод координат в пространстве.
§ 1. Координаты точки и координаты вектора.
1. Закончите предложения и заполните пропуски.
1. Прямоугольная система координат в пространстве задаётся тремя попарно перпендикулярными прямыми, пресекающимися в одной точке О - ____________________; направлением, выбранным по каждой прямой и единицей измерения отрезков. Прямые с выбранными направлениями называются ___________________________________________. Их обозначения 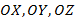 и соответственно название: ось абсцисс, ось ______________________ и ось ______________________.
и соответственно название: ось абсцисс, ось ______________________ и ось ______________________.
Координатные плоскости обозначаются: 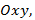 _____________
_____________
______________. Точка О разделяет каждую из осей координат на 2 луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч - ________________________________________________.
В прямоугольной системе координат каждой точке А пространства сопоставляется тройка чисел, которые называются её __________________________________________________.
2. Дано: 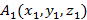 и
и 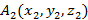 , тогда расстояние между двумя точками вычисляется по формуле:
, тогда расстояние между двумя точками вычисляется по формуле:
∣ 
3. Пусть 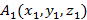 и
и 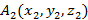 - произвольные точки, точка
- произвольные точки, точка 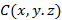 середина отрезка
середина отрезка 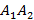 , тогда координаты середины отрезка находятся по формулам:
, тогда координаты середины отрезка находятся по формулам:
 =______________________
=______________________
4. Каждая координата суммы двух или более векторов равна _
_____________________________ соответствующих координат этих векторов, т. е. если 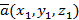 ,
,  , то координаты вектора
, то координаты вектора  _________________________________
_________________________________
_____________________________________________________.
5. Каждая координата разности двух или более векторов равна ___________________________________________________
соответствующих координат этих векторов, т. е. если 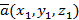 ,
,  , то координаты вектора
, то координаты вектора  ____
____
_____________________________________________________.
6. Каждая координата произведения вектора  , на число
, на число 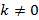 равна ______________________ соответствующей координаты вектора на это число, т. е. вектор
равна ______________________ соответствующей координаты вектора на это число, т. е. вектор 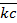 имеет координаты __________________________________________.
имеет координаты __________________________________________.
2. Ответьте на вопросы.
1. Какие из точек 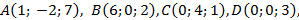
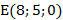 лежат:
лежат:
1) в плоскости 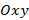 ____________________________________,
____________________________________,
2) на оси 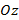 __________________________________________,
__________________________________________,
3) в плоскости  ____________________________________,
____________________________________,
4) в плоскости 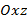 ____________________________________.
____________________________________.
2. Какие координаты (в общем виде) имеют точки, лежащие:
1) на оси 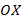 :
: 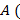 ______________________________________),
______________________________________),
2) на оси 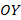 :
: 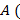 ______________________________________),
______________________________________),
3) на оси  :
: 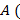 ______________________________________),
______________________________________),
4) на плоскости 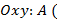 _______________________________),
_______________________________),
5) на плоскости 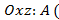 _______________________________),
_______________________________),
6)на плоскости 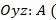 _______________________________),
_______________________________),
3. Как найти расстояние от точки 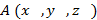 до начала координат в системе
до начала координат в системе 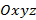 ?
?
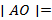 ______________________________________________.
______________________________________________.
4. Зная координаты векторов если 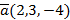 ,
, 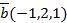 и
и 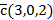 , найдите координаты векторов:
, найдите координаты векторов:
1) 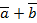 = ____________________________________________
= ____________________________________________
2) 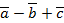 = _________________________________________
= _________________________________________
3) 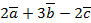 =______________________________________
=______________________________________
_____________________________________________________
5. Зная координаты точек 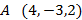 и
и 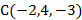 , найдите координаты вектора
, найдите координаты вектора 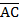 = _______________________________
= _______________________________
_____________________________________________________
6. Вычислите длину вектора 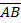 , если
, если  и
и 
__________________________________________________________________________________________________________
3. Выполните задания.
1. Постройте точки  ,
, 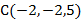 ,
, 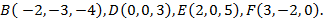
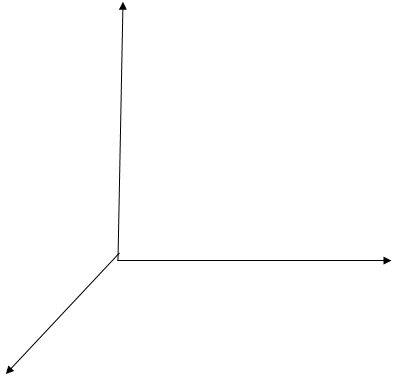 |
2. Найдите расстояние между двумя точками
1) 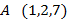 и
и 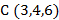 ,
,
2) 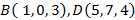 .
.
Решение:
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3. Найдите расстояние от точки 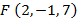 до осей координат.
до осей координат.
Решение:
1) до оси 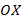 : _________________________________________
: _________________________________________
2) до оси 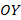 : __________________________________________
: __________________________________________
3) до оси  : __________________________________________
: __________________________________________
4. Отрезок 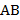 задан концом
задан концом  и серединой
и серединой  . Найдите координаты конца отрезка
. Найдите координаты конца отрезка  /
/
Решение:
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5. Найдите периметр треугольника, образованного векторами 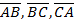 , если
, если 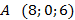 ,
, 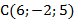 ,
, 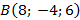 .
.
Решение:
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Докажите, что четырёхугольник с вершинами 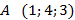 ,
,  ,
, 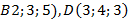 - параллелограмм.
- параллелограмм.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|