ВЕЧНЫЙ МАГНИТО-ГРАВИТАЦИОННЫЙ МОТОР

ВЕЧНЫЙ МАГНИТО-ГРАВИТАЦИОННЫЙ МОТОР

Канарёв Ф.М.

kanarevfm@mail.ru

Анонс. Физико-механический анализ процесса работы вечного магнито-гравитационного мотора показывает, что он базируется на элементарном взаимодействии магнитных и гравитационных сил, которое надлежит изучать в школе.

Заявка на патентование вечного магнито-гравитационного мотора была подана впервые в 1823г, то есть около 200 лет назад (рис. 1), а описание устройства опубликовали в 1927г. (рис. 2).

Рис. 1. Заявка на патентование магнито-гравитационного мотора была подана в 1823г

Рис. 2. Авторы магнито-гравитационного мотора

опубликовавшие информацию о нём в 1927г

На фото (рис. 3) представлена действующая модель магнито-гравитационного мотора [1]. Физику процесса его работы ещё никому не удалось описать. Попытаемся сделать это, руководствуясь новыми законами механодинамики и электродинамики [1].

а)

Рис. 3: а) – фото магнито-гравитационного мотора;

b) –магнито-гравитационный мотор вращается под действием магнита и силы гравитации

Итак, физика процесса работы магнито-гравитационного мотора остаётся не выявленной с 1823 года в условиях её простоты. Колесо магнито-гравитационного мотора вращается за счёт взаимодействия магнита с вращающимся шариком, который вращает колесо мотора. Из этого следует, что секрет вращения шарика, а значит и колеса, скрыт в направлении магнитных силовых линий, которые формируются магнитным полем между постоянным магнитом и наведённым магнитным полем в шарике [2].

Мы уже давно показали, что все электромоторы и электрогенераторы работают благодаря формированию магнитных силовых линий между магнитными полюсами роторов и статоров [2]. Представим ещё раз этот момент новой электродинамики. На рис. 4 показано направление магнитных силовых линий между одноимёнными и разноимёнными магнитными полюсами постоянных магнитов [2].

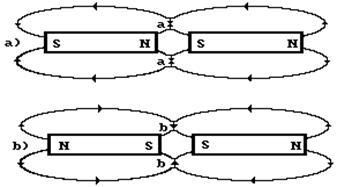
Рис. 4. Схема взаимодействия магнитных силовых

линий стержневых магнитов

Как видно (рис. 4, а), у разноименных магнитных полюсов, сближающих друг друга, магнитные силовые линии в зоне контакта полюсов (рис. 4, а, точки а) направлены навстречу друг другу 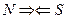, а у одноименных магнитных полюсов, отталкивающих друг друга (рис. 4, b, точки b), направления магнитных силовых линий в зоне контакта полюсов совпадают 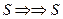[2].

Известно, что если постоянный магнит взаимодействует с деталью из железа, то внутри этой детали формируется магнитное поле с магнитной полярностью противоположной магнитной полярности постоянного магнита и железная деталь сближается с постоянным магнитом благодаря тому, что магнитные силовые линии в каждой точке магнитного поля между магнитом и железной деталью направлены на встречу друг другу (рис. 4, а). Именно в этом заключается физическая суть работы магнито-гравитационного мотора (рис. 3). Чтобы убедиться в этом представим схему взаимодействия магнитных полей постоянного магнита и шарика магнито-гравитационного мотора (рис. 5) [1]. При этом обратим внимание на то, что шарик взаимодействует с южным магнитным полюсом (конец магнита красного цвета) постоянного магнита (рис. 3, 5).

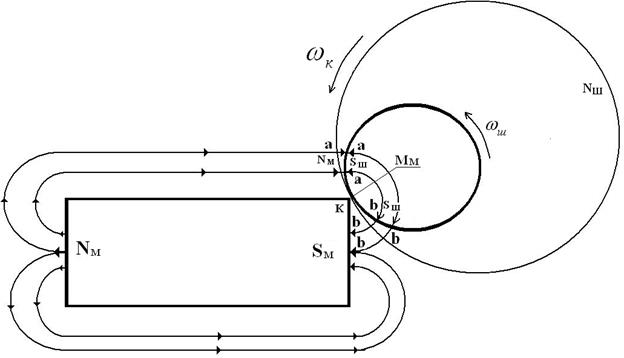
Рис. 5. Схема взаимодействия магнитных полей полюсов контакта

шарика и постоянного магнита

Итак, авторы магнито-гравитационного мотора (рис. 3, 5) сконструировали его так, что шарик, находящийся на внутренней поверхности обода вращающегося колеса, взаимодействует с острым углом южного (S) полюса магнита. В видео он окрашен в красный цвет [1]. Давно условились, считать, что магнитные силовые линии выходят из северного магнитного полюса постоянного магнита 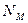и входят в его южный магнитный полюс 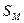(рис. 5).

При сближении магнита с намагничеваемой деталью, у неё, в зоне сближения, формируется магнитный полюс противоположной полярности. В нашем примере в тело шарика входят магнитные силовые линии северного магнитного полюса постоянного магнита (рис. 5). В результате в зоне их входа в тело шарика в нём автоматически формируется магнитный полюс противоположной полярности, то есть, южный магнитный полюс 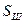, а с противоположной стороны шарика – северный магнитный полюс 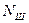(рис. 5).

Как видно (рис. 5), магнитные силовые линии северного полюса постоянного магнита 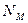и южного полюса шарика 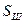направлены навстречу друг другу, как и в зоне (а….а) разноимённых магнитных полюсов постоянных магнитов (рис. 4, а). Так как разноимённые магнитные полюса постоянных магнитов сближаются в этом случае, то аналогично направленные магнитные силовые линии постоянного магнита и шарика в зонах (а…а) (рис. 5) сформируют магнитный момент, который будет поворачивать шарик относительно точки 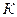- точки с наименьшим зазором между постоянным магнитом и шариком, против часовой стрелки (рис. 5). В зоне (b…b) шарика направления магнитных силовых линий, выходящих из его тела будут совпадать с направлением силовых линий постоянного магнита, входящих в его южный магнитный полюс 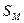. В результате в этой зоне взаимодействия магнитных полей шарика и постоянного магнита согласно рис. 4, b (зона b…b) сформируются силы, которые будут отталкивать тело шарика от тела постоянного магнита и таким образом – увеличивать суммарный магнитный момент 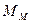, вращающий шарик, относительно точки 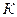(рис. 5). Так как момент сил взаимодействия шарика с внутренней поверхностью обода колеса (рис. 3 и 5) будет больше момента сил гравитации, вращающих шарик в обратном направлении, то шарик будет вращаться и вращать колесо магнито-гравитационного мотора, против хода часовой стрелки [1]. Составим уравнение сил и моментов, описывающих процесс работы магнито-гравитационного мотора (рис. 6).

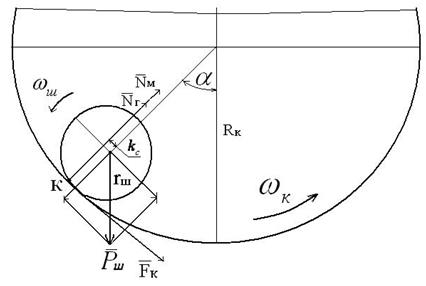
Рис. 6. Схема к расчёты силы сопротивления качению шарика,

формируемой силой гравитации

На рис. 6 к шарику приложены следующие силы: сила гравитации 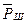; нормальная составляющая реакции поверхности колеса 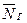, генерируемая силой гравитации 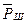; нормальная составляющая реакции поверхности колеса 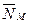, генерируемая магнитной силой, прижимающей шарик к внутренней поверхности колеса; касательная сила сопротивления качению шарика по внутренней поверхности колеса .

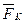Давно условились представлять коэффициент сопротивления качению колёс в виде плеча 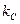(рис. 6) сдвига нормальной реакции от оси колеса в сторону его вращения и назвали это плечо коэффициентом сопротивления качению. Для стального шарика, катящегося по стали, он близок к величине 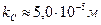. Обозначая радиус шарика символом 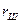, имеем сумму моментов сил, действующих на шарик при его качении по внутренней поверхности колеса (рис. 6).

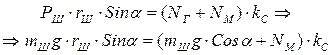. (1)

Из этого уравнения можно определить нормальную составляющую 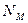, действующую на шарик, которая формируется магнитными силами, прижимающими шарик к внутренней поверхности колеса (рис. 6).

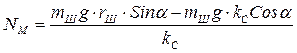. (2)

Если допустить, что при установившемся режиме работы магнито-гравитационного мотора его колесо и шарик вращаются равномерно, то можно вычислить кинетические энергии вращения колеса и шарика. Момент инерции 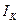вращающегося колеса определяется экспериментально, а момент инерции шарика равен 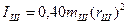. Обозначая в установившемся режиме угловые скорости колеса 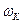и шарика 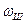, имеем математическую модель для расчёта суммарной кинетической энергии 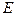вращающегося колеса 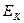и шарика .

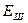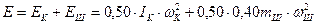. (3)

Вполне естественно, что есть основания полагать, что при равномерном вращении колеса и шарика их кинетические энергии, примерно, равны. Тогда появляется возможность определить момент инерции 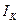колеса.

. (4)

Начальные исходные уравнения позволяют перейти к более глубокому описанию процесса работы магнито-гравитационного мотора и к созданию коммерческих моделей.

12 Следующая ⇒