
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Краткое содержание лекции. Задание на СРС. Задание на СРСП. Глоссарий
| Казахская Головная Архитектурно-Строительная Академия Активный раздаточный материал Математика I ФОЕНП Кредит 3 1 семестр Лекция №13 «Первообразная. Неопределенный интеграл » 2011-2012 уч. год К.т.н,, ассоц. проф. Сыдыкова Д.К. |
Краткое содержание лекции
1.Первообразная. Неопределенный интеграл его свойства.
Определение. Пусть функция 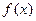 определена на некотором (конечном или бесконечном) интервале
определена на некотором (конечном или бесконечном) интервале 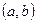 . Тогда функция
. Тогда функция 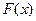 называется первообразной для функции
называется первообразной для функции 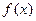 на интервале
на интервале 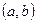 , если
, если 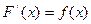 для всех
для всех 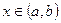 .
.
Зная только одну первообразную 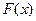 для функции
для функции 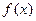 , находим множество всех первообразных для этой функции, которое совпадает с множеством функции вида
, находим множество всех первообразных для этой функции, которое совпадает с множеством функции вида 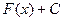 , где С -произвольная постоянная.
, где С -произвольная постоянная.
Обозначения: 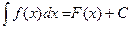 .
.
Основные свойства неопределенного интеграла:
10. 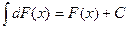 ; 20.
; 20. 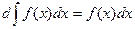
30. 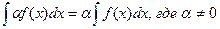
40. 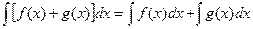
50. Если 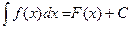 , то
, то 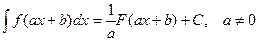 .
.
2. Основные формулы интегрирования.
Следующие интегралы обычно называются табличными интегралами:
1. 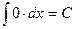 7.
7. 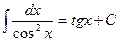
2. 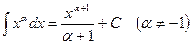 8.
8. 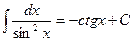
3. 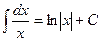 9.
9. 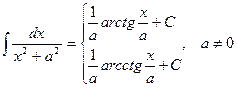
4. 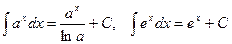 10.
10. 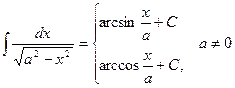
5. 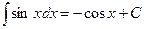 11.
11. 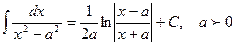
6. 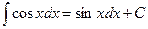 12.
12. 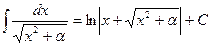
2. Интегрирование посредством разложения подынтегральной функции на слагаемые.
Рассмотрим этот метод на примере:
Пример 1. 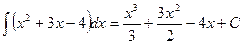
3. Интегрирование посредством замены переменной.
Пусть требуется вычислить интеграл 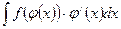 , при этом функции
, при этом функции 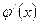 и
и 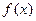 непрерывны на заданном интервале. Тогда этот интеграл можно упростить с помощью подстановки
непрерывны на заданном интервале. Тогда этот интеграл можно упростить с помощью подстановки 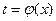 , используя равенство
, используя равенство
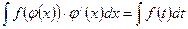 . Эта формула называется формулой замены переменной в неопределенном интеграле.
. Эта формула называется формулой замены переменной в неопределенном интеграле.
4. Интегрирование по частям.
Пусть производные функций 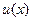 и
и 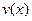 существуют и непрерывны на заданном интервале. Тогда имеет место равенство:
существуют и непрерывны на заданном интервале. Тогда имеет место равенство:

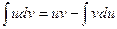 .
.
Эта формула называется формулой интегрирования по частям.
Задание на СРС
1. Таблица основных интегралов (конспект) [1, 3].
2. Решение задач по теме [ 2. ИДЗ – 7.1 c ].
Задание на СРСП
1. Интегрирование функций
Контрольные вопросы:
А. Для письменного контроля
1. Определение первообразной, неопределенный иентеграл и его основные свойства.
2. Методы интегрирования.
3. Основные формулы интегрирования.
Б. Для компьютерного тестирования
1. Найдите интеграл 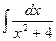 :
:
A) 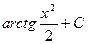 B)
B) 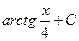 C)
C) 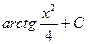 D)
D) 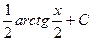 E) ln|x2 + 4|+C
E) ln|x2 + 4|+C
2. Найдите интеграл 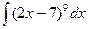 : A)
: A) 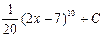 B) 9(2x –7)8+C
B) 9(2x –7)8+C
C) 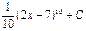 D)
D) 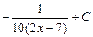 ; E)
; E) 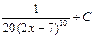
3. Найдите интеграл 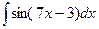 : A) -
: A) - 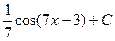 B)
B) 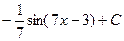 C) sin(7x-3)+C
C) sin(7x-3)+C
D) 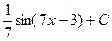 ; E)
; E) 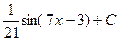
Глоссарий
| Казахский | Русский | Английский |
| Алғашқы функция | Первообразная функция | Antiderivative |
| Анықталмаған интеграл | Неопределенный интеграл | Ndefinite integral |
| Айнымалы ауыстыру | Замена переменной | Transformation of variable |
| Бөлшектеп интегралдау | Интегрирование по частям | Integration by parts |
| Интеграл астындағы функция | Подынтегральная функция | Integrand |
Используемая литература.
Основная:
1. Н.С. Пискунов. «Дифференциальное и интегральное исчисления» для ВТУЗов, 1 том, М.:Наука, 1998, 552стр.
2. К. Кабдыкаир. Курс математики. Алматы, 2005.
3. А.П. Рябушко «Индивидуальные задания по высшей математике». Ч.2 Минск, высшая школа, 2002, 14-104 стр.
4. Д.К. Сыдыкова Математика-1. Методическое руководство по выполнению заданий для СРС. КазГАСА, 2008.
Дополнительная:
5. Г.Н. Берман. «Сборник задач по курсу математического анализа». М.Наука, 2001, 384 стр.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|