б) Начертите на том же рисунке другую прямую d. Так как эта прямая параллельна оси Ох, то (смотри правило 1а выше) ее уравнение у= -3.

Урок алгебры в 7 классе 17.04.20

Тема урока. Линейное уравнение с двумя переменными и его график

1. Дата. Классная работа. Тема. Сегодня работаем по графикам из рисунка по учебнику. Эта тема важна для сдачи экзамена ОГЭ в 9 классе.

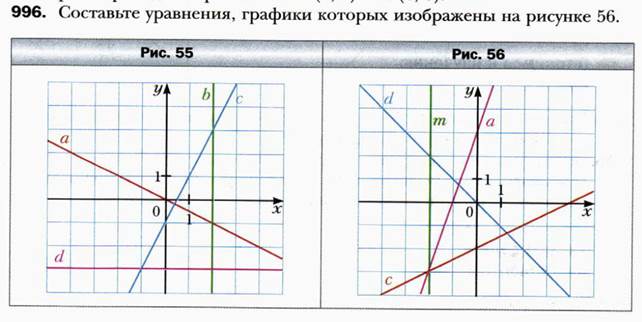
2. № 996. Составить линейное уравнение по заданному графику.

НАПОМНЮ

1) Проще всего составить уравнение по графику, параллельному

а) оси Ох. В этом случае у = а (а — некоторое число на оси Оу) , а х — любое.

Уравнение у = а — искомое (например у = 2 , у = -7 и т.д)

б) оси Оу. В этом случае х = b (b — некоторое число на оси Оx) , а y — любое.

Уравнение x = b — искомое (например x = 3,5 , x = -4 и т.д)

2) Если график не параллелен ни одной оси, то уравнение составляем в виде

у = kx + b

Если данный график пересекает ось Оу в точке сцелой ординатой, то b равно этой ординате.

Далее выбираем одну точку с целыми координатами и подставляем ее координаты в записанное уравнение, находим k.

Решение по рисунку 55.

1. Начертите систему координат и добавляйте в нее по одному графику в процессе решения.

а) Начертите на своем рисунке самую простую прямую b. Так как эта прямая параллельна оси Оу, то (смотри правило 1б выше) ее уравнение х = 2

б) Начертите на том же рисунке другую прямую d. Так как эта прямая параллельна оси Ох, то (смотри правило 1а выше) ее уравнение у= -3.

в) Начерти на том же рисунке следующую, чуть более сложную прямую а. Так как эта прямая проходит через начало координат, то ее уравнение имеет вид у = kx. Для нахождения коэффициента k выберем на прямой какую- нибудь точку, например

(-2;1) (здесь х -2, а у = 1) и подставим их в указанное уравнение, получим 1 = -2k, откуда k = -0,5. Значит, искомое уравнение имеет вид у = - 0,5х.

г) Начерти последнюю прямую с. Для того, чтобы ее начертить, сразу же определим необходимые точки, лежащие на этой прямой, первая точка — точка, лежащая на оси Оу,

это точка (0;-1) , а вторая, например, (1;1). Уравнение ищем в виде y = kx + b. Исходя из координат 1 точки, находим b = -1. Значит, искомое уравнение уже имеет вид y = kx – 1. Теперь подставим в него координаты второй точки

1 = k·1 - 1, решая его, найдем k = 2. Таким образом, искомое уравнение у = 2х - 1.

2. Решение по рисунку 56 выполни самостоятельно по записанному образцу. Пришли это решение с подробным объяснением до 14.00ч 17.04.20

Домашнее задание. № 997, 1002. Задание прислать до 12.00ч 18.04.20