
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задач по теме «Перпендикулярность в пространстве» часть 3
Решение задач по теме «Перпендикулярность в пространстве» часть 3
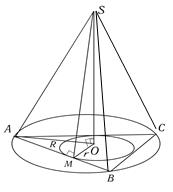
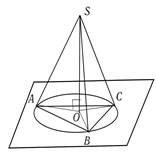 1) Из точки S вне плоскости проведены к ней три равные наклонные SA, SB, SC и перпендикуляр SO. Докажите, что основание перпендикуляра О является центром окружности, описанной около треугольника АВС
1) Из точки S вне плоскости проведены к ней три равные наклонные SA, SB, SC и перпендикуляр SO. Докажите, что основание перпендикуляра О является центром окружности, описанной около треугольника АВС
Дано: 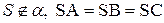 - наклонные
- наклонные
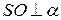
Доказать: О – центр окружности 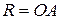
Доказательство
1) 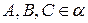 , строим
, строим 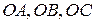
2) Рассмотрим 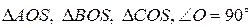 , так как
, так как 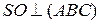
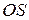 - общий катет,
- общий катет, 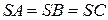 - по условию
- по условию 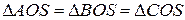 - по катету и гипотенузе. Значит,
- по катету и гипотенузе. Значит, 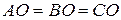 , то есть т. О – равноудалена от вершин
, то есть т. О – равноудалена от вершин 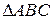 - центр окружности, описанной около
- центр окружности, описанной около 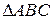 .
.
2) К плоскости треугольника из центра вписанной в него окружности радиуса 0,7 м восстановлен перпендикуляр длиной 2,4 м. Найти расстояние от концов этого перпендикуляра до сторон треугольника
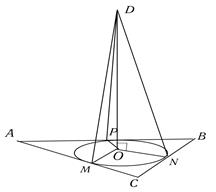
Дано:
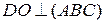 ,
, 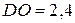 м
м
Окр ( 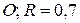 м)
м)
Найти: 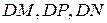
Решение
1) Построим радиусы вписанной в треугольник АВС 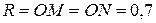 м;
м; 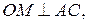
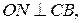
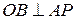
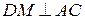 ,
, 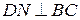 ,
,  по теореме о 3-х перпендикулярах
по теореме о 3-х перпендикулярах
Рассмотрим плоские треугольники в соответствующих плоскостях 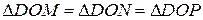 (по двум катетам – катет DO –общий а остальные – радиусы вписанной окружности), откуда
(по двум катетам – катет DO –общий а остальные – радиусы вписанной окружности), откуда 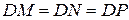
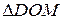 :
:  м. Ответ : 2,5 м.
м. Ответ : 2,5 м.
Вывод :
Пусть 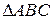 - произвольный
- произвольный
1) 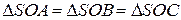 , если
, если 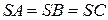
О – точка пересечения биссектрис – центр вписанной и описанной окружностей
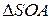
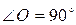 , где
, где 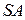 - расстояние до вершины треугольника АВС
- расстояние до вершины треугольника АВС
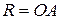 - радиус описанной окружности
- радиус описанной окружности
2) 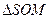 , где
, где 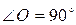
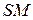 - расстояние до стороны треугольника АВС
- расстояние до стороны треугольника АВС 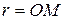 - радиус вписанной окружности
- радиус вписанной окружности
1) Если расстояния от вершины  до вершин
до вершин 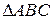 равны, то
равны, то 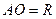 , радиус описанной около треугольника АВС окружности, где
, радиус описанной около треугольника АВС окружности, где 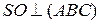
2) Если расстояние от точки  до сторон
до сторон 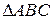 равны, то
равны, то 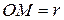 радиус вписанной в треугольник АВС окружности, где
радиус вписанной в треугольник АВС окружности, где 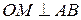
3) Расстояния от точки S до всех сторон квадрата равны а. Найти расстояние от точки S до плоскости квадрата, если диагональ квадрата равна d.
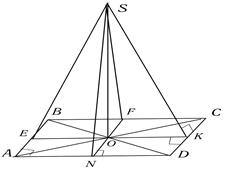
Дано : 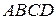 - квадрат
- квадрат
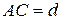

Найти : 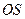 .
.
Решение
1) 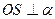 - искомое расстояние
- искомое расстояние 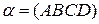
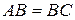
2) 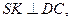
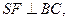
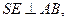
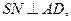 по теореме о трех перпендикулярах
по теореме о трех перпендикулярах 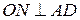 ,
, 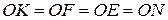 - как проекции равных наклонных. О – центр окружности вписанной в квадрат
- как проекции равных наклонных. О – центр окружности вписанной в квадрат 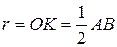 (так как радиус вписанной в квадрат окружности рамен половине стороны квадрата)
(так как радиус вписанной в квадрат окружности рамен половине стороны квадрата)
АВ найдем из 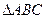 ,
, 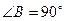 ,
, 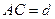
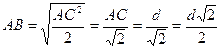
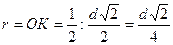
Из 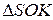 :
: 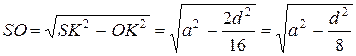 Ответ:
Ответ: 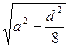
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|