Контакты

Случайная статья

Задачи для подготовки к экзамену , 1 курс, 1 семестр, 2012-2013 уч. г.

Задачи для подготовки к экзамену , 1 курс, 1 семестр, 2012-2013 уч. г.

1. Решить систему (по формулам Крамера или методом Гаусса)

2. Найти матрицу, обратную к данной .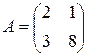

3. Решить матричное уравнение .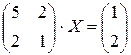

4. Определить, при каком 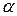коллинеарны векторы 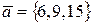и .

5. Доказать, что векторы ортогональны , .

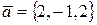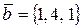6. Проверить, являются ли векторы компланарными , , .

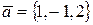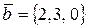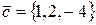7. Найти определитель .

8. Проверить, лежат ли точки 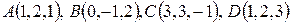в одной плоскости.

9. Найти векторное произведение 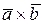, если .

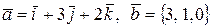10. Найти скалярное произведение 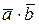, если .

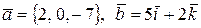11. Найти смешанное произведение , если .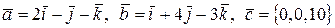

12. Найти площадь параллелограмма (или треугольника), построенного на векторах .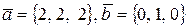

13. Найти объем пирамиды, вершины которой лежат в точках .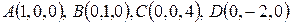

14. Найти скалярное произведение 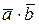, если .

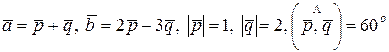15. Найти 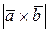, если .

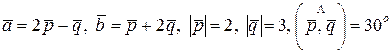16. Составить уравнение плоскости, проходящей через точку 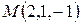перпендикулярно:

а) вектору ,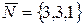

б) прямой .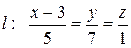

17. Написать канонические уравнения прямой, проходящей через точку 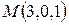параллельно:

а) вектору ,

б) плоскости ,

в) прямой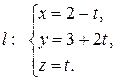

18. Написать параметрические уравнения прямой, проходящей через две точки .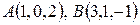

19. Найти точку пересечения прямой 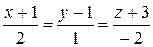и плоскости .

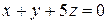20. Найти точку пересечения двух прямых 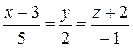и .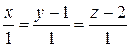

21. Определить вид кривой второго порядка:

а) ,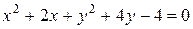

б) ,

в) .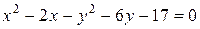

22. Вычислить пределы (можно по правилу Лопиталя):

а) ,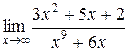

б) ,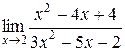

в) ,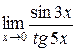

г) .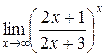

23. Найти производные функций:

а) ,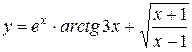

б) ,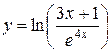

в) ,

г) ,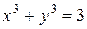

д)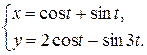

24. Найти интегралы (метод замены переменной):

а)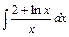

б)

в)

г)

д)

е)

ж)

з)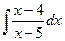

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.