Решение задач по теме «Перпендикулярность в пространстве» Часть 1

Решение задач по теме «Перпендикулярность в пространстве» Часть 1

1) От столба высотой 3,9 м к дому прикреплен электрический провод на высоте 5,8 м. найти длину провода (без провисания), если расстояние от столба до дома составляет 3,4 м

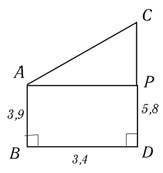
Дано: ,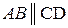

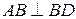
АВ = 3,9 м, СD = 5,8 м, ВD = 3,4 м

Найти: АС

Решение:

1) Строим 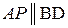, , 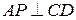так как 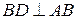, 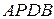- плоский прямоугольник

2) Рассмотрим , 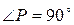по теореме Пифагора: 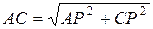, где 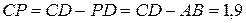м, то есть 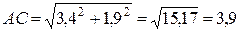м.

Ответ: 3,9 м

2) Из точки к плоскости проведены две наклонные, дины которых равны 10 см и 17 см, разность проекций этих наклонных составляет 9 см. Найти проекции наклонных

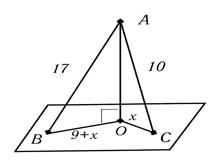
Дано: ,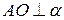

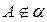
АВ, АС – наклонные

АС=10 см, АВ=17 см

ВО - ОС=9 см

Найти: ВО и ОС

Решение

1) Пусть плоскости , ,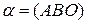

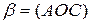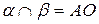
2) и - плоские прямоугодьные треугольники, где, соотвенно 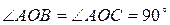и АО – общий катет

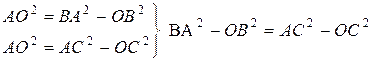
Пусть ОС = х (см), тогда ВО = х+9 (см). По теореме Пифагора имеем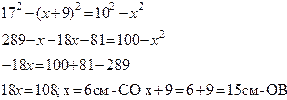

Ответ : 6 см и 15 см

3) Из точки к плоскости проведены две равные наклонные длиной 2 см, составляющие угол между собой 60⁰ . Проекции данных наклонных на плоскость перпендикулярны. Найти расстояние от точки до плоскости.

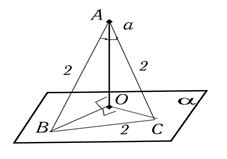
Дано:

АВ = АС = 2 м

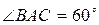
Найти: АО

Решение

Строим плоскость b (АВС) Рассматриваем 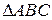: плоский равносторонний, так как 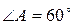и АВ = АС по условию, следовательно ВС=2см

Рассматриваем 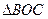в плоскости a, по условию задачи и из свойств равных наклонных следует, что в

По теореме Пифагора 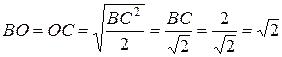м

По свойствам наклонной и перпендикуляра, проведенных из данной точки к плоскости имеем, что

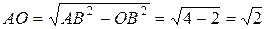м Ответ: 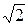м

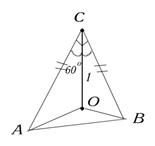4) Из точки, отстоящей от плоскости на расстоянии 1м, проведены две равные наклонные. Найти расстояние между основаниями наклонных, если известно, что наклонные перпендикулярны и образу ют с перпендикуляром к плоскости углы, равные 60⁰.

Дано: 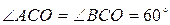, АС=СВ, 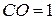м

Найти: АВ

Решение:

Строим плоскость b (АВС). Рассматриваем 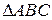: плоский прямоугольный равнобедренный с равными катетами по условию. По теореме Пифагора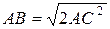

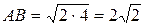Строим плоскость (АОС), где , По соотношениям в прямоугольном треугольнике находим м, следовательно (м) Ответ: 2 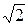м