Хелпикс

Главная

Контакты

Случайная статья



Тригонометрические функции двойного угла



Тригонометрические функции двойного угла

Положив в формуле

sin (α + β) = sin α • cos β + sin β • cos α.

β = α,мы получим:

sin 2α = sin α • cos α + sin α • cos α = 2 sin α cos α.

Итак,

sin 2α = 2 sin α cos α (1)

Синус двойного угла равен удвоенному произведению синуса данного угла на его косинус.

Аналогично, положив в формуле

cos (α + β) = cos α cos β — sin α sin β,

β = α, получим:

cos 2α = cos α cos α—sin α sin α= cos 2 α — sin 2 α.

Итак,

cos 2α = cos 2 α — sin 2 α. (2)

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла

Эту формулу можно преобразовать

cos2α = cos2α-sin2α = 1-sin2α-sin2α = 1-2sin2α.

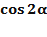 = cos2α-sin2α = cos2α-(1-cos2α) =2cos2α-1.

Точно так же, положив в формуле

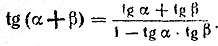
β = α, получим:

Тангенс двойного угла равен удвоенному тангенсу данного угла, деленному на единицу минус квадрат тангенса того же угла.

Примеры.

1) Пусть sin α = 0,6, причем угол α оканчивается во 2-й четверти

Вычислить:.sin 2α, cos 2α

 Тогда cos α = — \/1 — sin2 α = — \/ 1 — 0,36 = — 0,8.

Поэтому

sin 2α = 2 sin α • cos α = 2 • 0,6 • (— 0,8) = — 0,96;

cos 2α = cos 2 α — sin 2 α = 0,64 — 0,36 = 0,28.

2) Пусть tg α = 3. Тогда

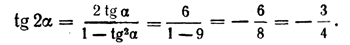
Замечание. Не следует думать, что двойной угол обязательно содержит четное число градусов или радианов: 20°; 60°; 4; 6 и т. д. Под двойным углом можно понимать любой угол. Например,

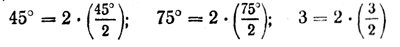
и т. д., вообще, α = 2 • α/2.

Выразить синус, косинус или тангенс, используя формулы двойного угла
1) sin 48°;
2) cos 164°;
3) tg 92°;

 

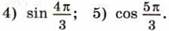
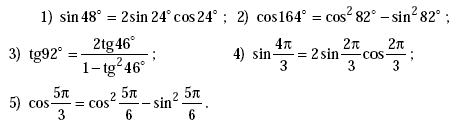
Поэтому иногда доказанные выше формулы полезно записывать в виде:

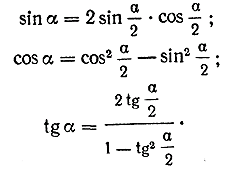
Эти формулы выражают тригонометрические функции угла через тригонометрические функции половинного угла

Вычислить:

1)

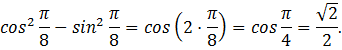
2)

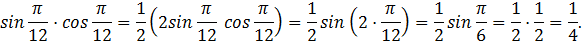
3)

4. Дано: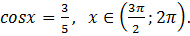

Найти: а) 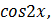б)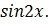

Решение:

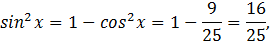
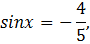
Учитывая, ч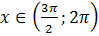то , то

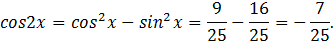
Ответ: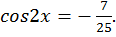

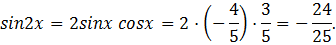
Ответ: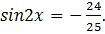

5. Упростить:

а) 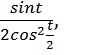б)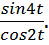

Решение:

а)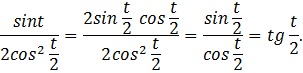

Ответ: .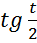

б)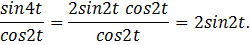

Ответ: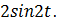

5. Вычислить, не используя калькулятор.

2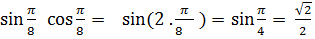

Самостоятельно:

1. №500, №501, №503, №504, №506,№507
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.