Задача № 1. Расчет линейной электрической цепи постоянного тока. Параметры цепи для варианта № 6. Преобразование цепи. Уравнения по законам Кирхгофа. Метод контурных токов. Метод узловых потенциалов

Задача № 1

Расчет линейной электрической цепи постоянного тока

Таблица 1.1

Параметры цепи для варианта № 6

Источники ЭДС и тока:				E₂ = 250 B; E₄₁ = 100 B; J₁ = J₂ = 10 A
Сопротивления резисторов
R₁, Ом	R₂, Ом	R₃, Ом	R₄₁, Ом		R₄₂, Ом	R₅, Ом	R₆, Ом
	-				-

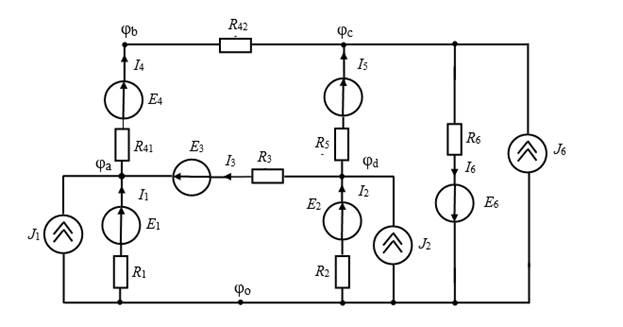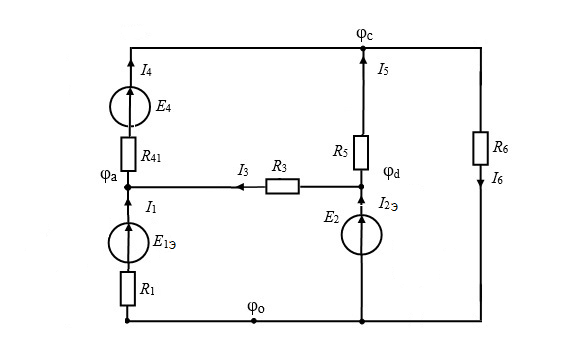
Рис. 1.1. Обобщенная схема цепи.

1. Преобразование цепи

Сложную разветвленную цепь необходимо преобразовать в более простую, превратив токи J в эквивалентные ЭДС.

Рис. 1.2. Непреобразованная цепь для варианта № 6

a) Участок 1.

Необходимо преобразовать ток J₁ в эквивалентную ЭДС E₁_Э:

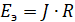
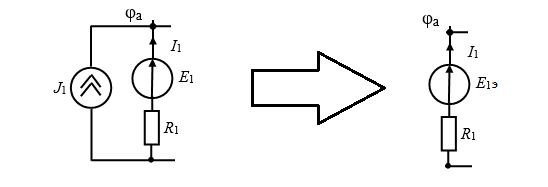
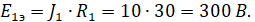
b) Участок 2.

На участке нет активной нагрузки, однако ток J₂ параллелен току I₂,

тогда можно сложить их, получив эквивалентный ток I_2Э:

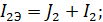
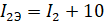
Таким образом получаем преобразованную схему цепи.

Рис. 1.3. Преобразованная схема цепи.

2. Уравнения по законам Кирхгофа

I закон Кирхгофа:

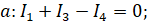
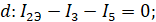
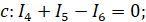
II закон Кирхгофа.

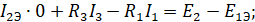
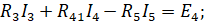
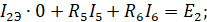
3. Метод контурных токов

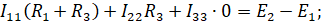
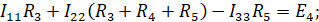
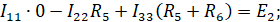
Если подставить известные значения, получим систему уравнений:

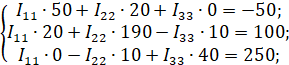
Ее можно преобразовать в матрицу:

		-50
	-10
-10

Решением матрицы являются контурные токи:

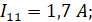
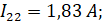
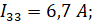
тогда:

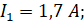
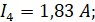
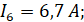
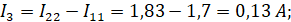
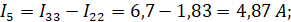
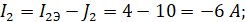
4. Метод узловых потенциалов

На участке 2 цепи отсутствует активное сопротивление, следовательно, невозможно найти его проводимость. При расчетах методом узловых потенциалов, потенциал j_d примем равным ЭДС E₂.

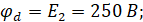
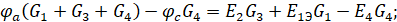
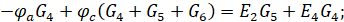
Нахождение проводимостей:

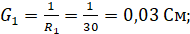
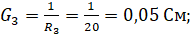
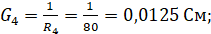
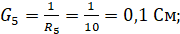
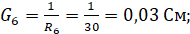
Подставляя известные значения получим систему уравнений:

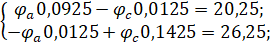
Преобразуем в матрицу:

0,0925	-0,0125	20,25
-0,0125	0,1425	26,25

Решением матрицы являются искомые потенциалы j_a и j_c:

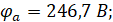
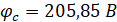
Нахождение токов:

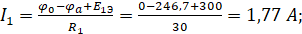
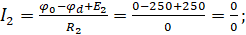
Ток I₂ методом узловых потенциалов найти невозможно, так как на участке 2 цепи отсутствует активное сопротивление.

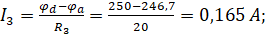
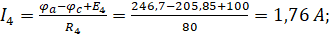
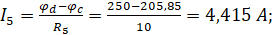
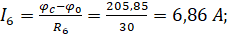
Получаем:

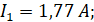
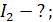
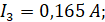
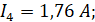
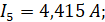
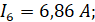
Таблица 1.2

Метод расчета	Рассчитанные параметры
Метод контурных токов	I₁₁ = 1,7 A, I₂₂ = 1,83 A, I₃₃ = 6,7 A
Метод контурных токов	I₁= 1,7 A	I₂= -6 A	I₃= 0,13 A	I₄= 1,83 A	I₅= 4,87 A	I₆= 6,7 A
Метод узловых потенциалов	j₀= 0 В, j_a= 246,7 B, j_c= 205,85 B, j_d= 250 B
Метод узловых потенциалов	I₁= 1,77 A	I₂= --- A	I₃= 0,165 A	I₄= 1,76 A	I₅= 4,415 A	I₆=6,85 A

12 Следующая ⇒