Тридцатое апреля. Классная работа. Длина отрезка. Длина окружности. Площадь круга

Тридцатое апреля

Классная работа

Длина отрезка

Отрезок – это часть прямой, ограниченная двумя точками.

Обозначение: отрезок АВ или отрезок с.

Любой отрезок имеет определённую длину, большую нуля.

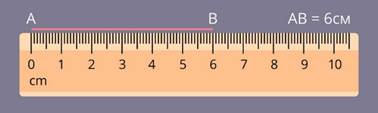
Длина может быть выражена натуральным или дробным числом.

Измерить отрезок – значит найти его длину.

Длина отрезка – это расстояние между его концами.

Свойства длин отрезков:

– равные отрезки имеют равные длины;

– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

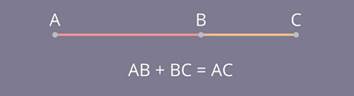
Единицы измерения длины в десятичной системе мер:

1 мм, 1 см, 1 дм, 1 м и т. д.

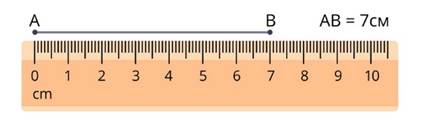
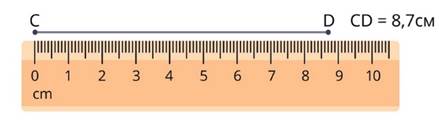
На практике используют приближённое значение длин отрезков, например, с точностью 0,1 или 0,01 части единичного отрезка, но точность приближения зависит от поставленной задачи.

№1027(а,в)

а) АВ = 3 = = 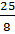3,125

АВ = 3,125 ≈ 3 (с точностью до 1 с недостатком)

АВ = 3,125 ≈ 3,1 (с точностью до 0,1 с недостатком)

АВ = 3,125 ≈ 3,12 (с точностью до 0,01 с недостатком);

в) АВ = 3 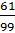= = 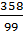3,6161…

АВ = 3,6161… ≈ 3 (с точностью до 1 с недостатком)

АВ = 3,6161… ≈ 3,6 (с точностью до 0,1 с недостатком)

АВ = 3,6161… ≈ 3,61 (с точностью до 0,01 с недостатком).

Длина окружности. Площадь круга

Окружность

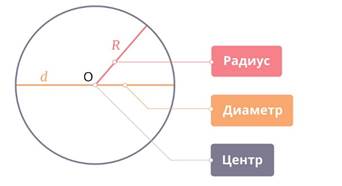Элементы окружности:

- центр

- радиус

- диаметр

Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которая называется центром окружности.

Отрезок, соединяющий две точки окружности, называется хордой.

Диаметр – это хорда, проходящая через центр окружности.

Ещё в древности было установлено, что какой бы ни была окружность, отношение её длины к её диаметру является постоянным числом. Сейчас это число обозначают греческой буквой π. (читается – «пи»)

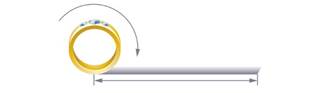
Как измерить дину окружности?

Можно взять сантиметровую ленту (если нет ленты, можно воспользоваться нитью или полоской бумаги).

Можно прокатить кольцо по ровной поверхности, сделав полный оборот.

Закон для более точного вычисления числа π очень сложен. В настоящее время значение π для точных расчётов в строительстве, авиационной или космической промышленности находят при помощи компьютера.

Вспомните, что π – это иррациональное число, которое выражается бесконечной непериодической дробью.

π = 3,141592653589793238…

При решении обычных задач используют приближенное значение

π ≈ 3,14 (иногда используют π ≈ 3)

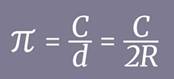Пусть С – длина окружности,

R – радиус

d – диаметр, тогда

С = πd

С = 2πR

Следовательно, справедливы формулы для вычисления длины окружности:

Круг – это часть плоскости, ограниченная окружностью.

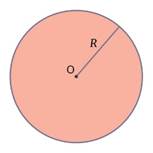
S = πR²

С помощью числа π вычисляют площадь круга:

№ 1. Радиус круга равен 5 см. Найдите длину окружности С, площадь круга S.

Решение:

R = 5см

С = 2πR = 2 ∙ 3,14 ∙ 5 = 31,4 (см).

S = πR² = 3,14 ∙ 5² = 3,14 ∙ 25 = 78,5 (см²).

Ответ: 31,4 см; 78,5 см.

№ 2. Как изменится длина окружности, если её радиус увеличить в 3 раза?

Решение:

R – радиус окружности, С – длина окружности

Было: С = 2πR

Стало: С₁ = 2π(2R) = 4πR = 2С

Ответ: длина окружности увеличится в 2 раза.

Домашнее задание: 1) чит. п.5.6, решить №1023, 1027(б,г)

2) чит. п.5.7, решить №1031(б), 1032(б), 1033(б).

(Каждый пункт ДЗ оценивается отдельно)