Векторные и скалярные величины. Действия над векторами.

1.4. Векторные и скалярные величины. Действия над векторами.

Физические величины, которые выражают только числом, называют скалярными или скалярами (а, b, c).

Физические величины, которые характеризуют числовым значением, направлением и геометрическим способом сложения, называют векторными или векторами (а, b, c).

Векторы а и b являются равными, если совпадают их модули и направления (рис. 1).

Если векторы а и b имеют одинаковые модули, и противоположные направления – их называют противоположными (рис. 2).

Если вектор умножить на скаляр, то получим вектор такого же направления, с модулем, равным произведению модуля вектора на скаляр.

Р = k*a.

Сумма векторов.

Правило параллелограмма.

Если векторы а и b имеют общее начало, то для получения их суммы необходимо построить на этих векторах параллелограмм, диагональ которого будет вектором суммы векторов а и b. (рис. 3)

Если в этом параллелограмме от конца вектора а до конца вектора b провести диагональ, то она будет равна разности векторов а и b. (рис. 4).

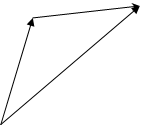
Правило треугольника.

Параллельным перенесением вектора b совместить его начало с концом вектора а, тогда вектором суммы с = а + b будет вектор, который объединяет начало вектора а и конец вектора b.

Когда векторы направлены вдоль одной прямой или параллельны их называют коллинеарными.

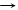
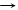
а b a b

a c a c a c

b b

⇐ Предыдущая 12