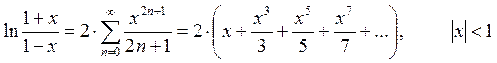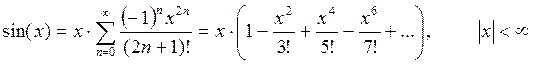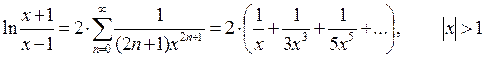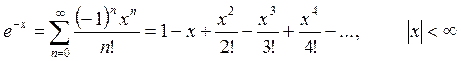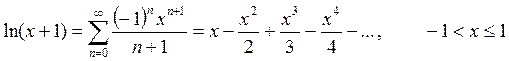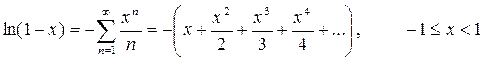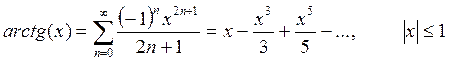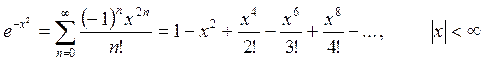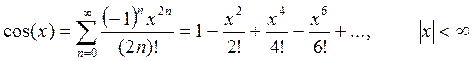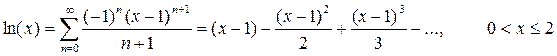- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Варианты для ЗАДАНИЯ 2 (создание рекурсивной функции)
Пример
Составить программу обработки динамической структуры данных: в стек, элементы которого упорядочены по возрастанию, вставить новый элемент так, чтобы сохранить упорядоченность.
Математическая модель:
На вход поступает несколько чисел типа Int, формирующих стек;
На выходе получаем отсортированный стек с добавленным пользователем элементом.
Код программного модуля:
#include "stdafx.h"
#include "iostream"
#include <time.h>
using namespace std;
struct stek
{
int d;
struct stek *next; // указатель на следующий элемент стека
};
void push(stek* &next, int d); // функция будет помещать элемент в стек
// next – указатель на вершину стека
int pop(stek* &next); // функция будет извлекать элемент из стека
// вершина которого - next
void push(stek* &next, int d)
{
stek *pv = new stek; // объявляем новую динамическую переменную типа stek
pv->d = d; // записываем значение, которое помещается в стек
pv->next = next; // связываем новый элемент стека с предыдущим
next = pv; // новый элемент стека становится его вершиной
}
int pop(stek* &next)
{
int temp = next->d; // извлекаем в переменную temp значение в вершине стека
stek *pv = next; // запоминаем указатель на вершину стека, чтобы затем
// освободить выделенную под него память
next = next->next; // вершиной становится предшествующий top элемент
delete pv; // освобождаем память, тем самым удалили вершину
return temp; // возвращаем значение, которое было в вершине
}
int output(stek* &next)
{
int out = next->d;
next = next->next;
return out;
}
void main()
{
srand(time(NULL));
int size, elem, k = 0, k2 = 0, k3 = 0;
stek *s1 = new stek;
stek *s2 = new stek;
stek *s3 = new stek;
cout << "Stack: ";
for (int i = 0; i < 10; i++)
{
elem = rand() % 50;
push(s1, elem);
cout << elem << " ";
k++;
}
cout << endl;
int max, tek;
while (k != 0)
{
max = pop(s1);
k--;
push(s2, max);
k2++;
while (k != 0)
{
tek = pop(s1);
k--;
if (tek > max) { max = tek; }
push(s2, tek);
k2++;
}
while (k2 != 0)
{
tek = pop(s2);
k2--;
if (tek == max){ push(s3, tek); k3++; }
else{ push(s1, tek); k++; }
}
}
cout << "Stack sort: ";
while (k3 != 0){
int o = output(s3);
cout << o << " ";
push(s1, o);
k++;
k3--;
}
k++;
cout << endl;
int el = 0;
cout << "Enter element: ";
cin >> el;
push(s1, el);
k2 = 0; k3 = 0;
while (k != 0)
{
max = pop(s1);
k--;
push(s2, max);
k2++;
while (k != 0)
{
tek = pop(s1);
k--;
if (tek > max) { max = tek; }
push(s2, tek);
k2++;
}
while (k2 != 0)
{
tek = pop(s2);
k2--;
if (tek == max){ push(s3, tek); k3++; }
else{ push(s1, tek); k++; }
}
}
while (k3 != 0){
cout << output(s3) << " ";
k3--;
}
cout << endl;
system("pause");
}
Варианты для ЗАДАНИЯ 2 (создание рекурсивной функции)
Указания:
Необходимо разработать программу, вычисляющую значение функции с помощью разложения в ряд. Сумма ряда должна вычисляться с помощью рекурсивной функции. Рекурсивная функция должна обязательно иметь хотя бы одну не рекурсивную ветвь, то есть заканчивать вычисления при некотором условии. Сходящийся числовой ряд будет достигать искомого значения при большом количестве суммируемых членов ряда. При этом разность между соседними членами последовательности станет очень мала. Будем считать, что необходимая точность вычислений достигнута, если разность между соседними элементами ряда меньше заданной точности (это и будет в данном случае условие выхода из рекурсивной функции). На каждом проходе нужно запоминать предыдущий член ряда. Следующий член ряда вычисляется через предыдущий (не используйте возведение в степень, вместо этого будет простое умножение). Для проверки полученного результата выведите на экран значение указанной функции (левую часть выражения), вычисленную с помощью рекурсии сумму ряда (правую часть выражения), а также количество просуммированных членов ряда.
Для сравнения рассмотрим вычисление факториала обычным способом (в цикле) и с помощью рекурсии. Факториал натурального числа n это произведение всех натуральных чисел от 1 до n, вычисляется по формуле: 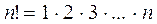
Итерация:
double Factorial(int n)
{
double F = 1;
for (int i = 0; i < n; i++)
F *= i;
return F;
}
Рекурсия:
double Factorial(int n)
{
if (n == 0) return 1;
else
return (n * Factorial(n-1));
}
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|