
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема «Понятие производной. Формулы и правила дифференцирования»
Тема «Понятие производной. Формулы и правила дифференцирования»
Задание №1.Изучите тему в учебнике на стр. 171-172 Занятие 3. Понятие производной.(п.1), стр. 174-175. Занятие 4. Формулы дифференцирования. Стр. 180 Занятие 5. Производные элементарных функций. Разберите примеры из учебника.
Задание №2. Перепишите в тетрадь следующую таблицу с разобранными примерами.
Задание 3. Выполните из учебника на стр. 182 Задание №5(примеры1,4,5,6) письменно в тетрадях. Из задачника стр. 235 №9.12А(1-11)
Присылаем работы в личных сообщениях, оформив работу по образцу
ФИО (в каждом конспекте пишем в начале) Иванов А.А.
Дата 24.03.2020
Тема «Понятие производной. Формулы и правила дифференцирования»
Формулы и правила дифференцирования
| № п/п | Формула | Пример |
| с' = 0 | 5' = 0; (-12) ' = 0; | |
| (kx) '= k | (6x) ' = 6; (-7x) '=-7; 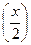 '= '= 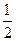 ; x' =1 ; x' =1
| |
| (x2) = 2x | ||
| (x3) = 3x2 | ||
| (x α ) = α · x α-1 | (x17) ' = 17x16 ; (x8) ' = 8x7 ; (x -5) ' = -5x -6 | |
( 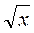 ) = ) = 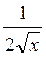
| ||
 = = 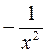
| ||
| (sin x) ' = cos x | ||
| (cos x) ' = -sin x | ||
(tg x) ' = 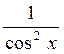
| ||
(ctg x) ' = 
| ||
(ln x) ' = 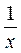
| ||
(loga x) ' = 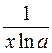
| ||
| (ex) '=ex | ||
| (ax) '=axlna | ||
| Правила | Пример | |
| (С · u) = C · u' | (5x2) ' = 5 · 2x = 10x; (7x3) = 7 · 3x2 = 21x2;  = = 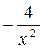 ; ; 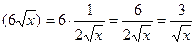
| |
| (u ± v ) = u ± v | (5x + x2 -1)’ = (5x)’ + (x2)’ – (1)’ = 5 +2x
(x15 - 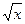 )’ = 15x14- )’ = 15x14- 
| |
| (u · v ) = u · v + v · u | (x3· 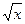 )' =(x3) '· )' =(x3) '· 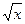 + ( + ( 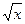 )'·x3=3x2· )'·x3=3x2· 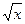 +
+ x3· +
+ x3· 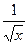
| |

| 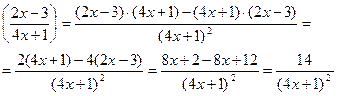
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|