Контакты

Случайная статья

ТЕМА «ПРОИЗВОДНАЯ». Законспектировать и разобрать ниже представленный теоретический и практический материал. Основные формулы дифференцирования. Правила дифференцирования. Практическая часть. Найдите производную. ЗАПИСАТЬ НИЖЕ ЗАДАНИЯ С РЕШЕНИЕМ И РАЗОБРА

Стр 1 из 2Следующая ⇒

ТЕМА «ПРОИЗВОДНАЯ»

1) Законспектировать и разобрать ниже представленный теоретический и практический материал

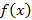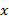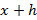ОПРЕДЕЛЕНИЕ: Пусть функция определена на некотором промежутке, – точка этого промежутка и число такое, что также данному промежутку. Тогда

предел разностного отношения 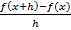при 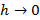, (если этот предел существует) называется производной функции 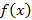в точке 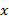и обозначается 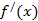(читается : «эф штрих от икс»). Таким образом,

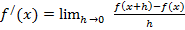. (1)

Если функция 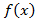имеет производную в точке 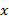, то эта функция называется дифференцируемой в этой точке.

Если функция 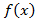имеет производную в каждой точке некоторого промежутка, то функция дифференцируема на этом промежутке.

Операция нахождения производной называется дифференцированием.

Основные формулы дифференцирования


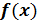
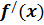
1.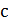
2.
3.		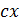c
4.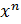
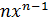
5.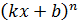
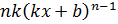
6.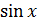
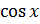
7.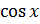
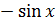
8.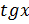
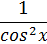
9.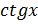
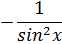
10.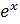
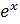
11.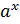
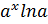
12.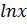
13.
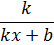
14.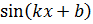
15.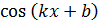
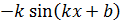
16.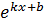

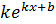
Правила дифференцирования

1) Постоянный множитель можно вынеси за знак производной

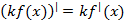
2) Производная суммы (разности) равна сумме (разности) производных

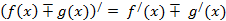
3) Производная произведения

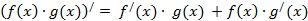
4) Производная частного

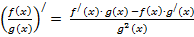
5) Производная сложной функции

.

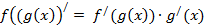Практическая часть

Найдите производную

а) ,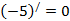

б) 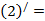0,

в) ,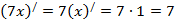

в) ,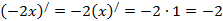

г) ,

д)

е) ,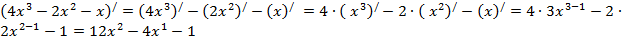

ж) ,

з) ,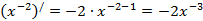

и) ,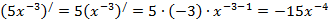

к)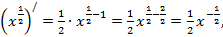

л) ,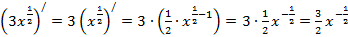

м)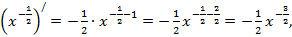

н) ,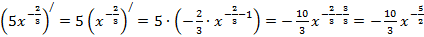

о) ,

п) ,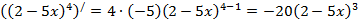

р) ,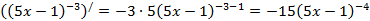

с) ,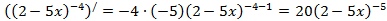

т) ,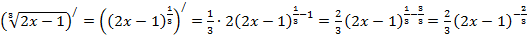

у) ,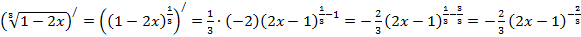

ф) ,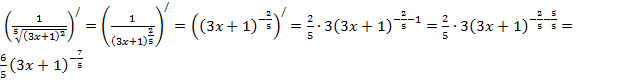

х) ,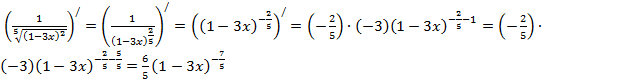

ц) ,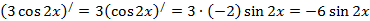

ч) ,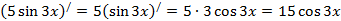

ш) ,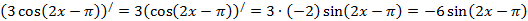

щ) ,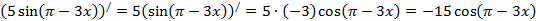

э) ,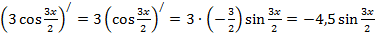

ю) ,

я) .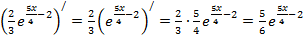

2) ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ИЗ УЧЕБНИКА СТРАНИЦА 238 - №787, №791

3) ЗАПИСАТЬ НИЖЕ ЗАДАНИЯ С РЕШЕНИЕМ И РАЗОБРАТЬ!!!! Выполнить ТОЛЬКО номера 806-807

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.