Просто посчитаем

Просто посчитаем

0) Из бочки с медом в бочку с дегтем переложили ложку меда. Затем перемешали и из бочки со смесью меда и дегтя переложили ровно такую же ложку в деготь. Чего теперь больше дегтя в меде или меда в дегте?

Решение:

Поскольку ложки перекладывали одинаковые, всего смеси в каждой из бочек ровно столько же сколько было в начале. Но при этом в первой бочке стало меньше меда пусть, например, на 100 мл. Значит, на месте этого меда теперь лежит 100 мл. дегтя. А соответственно не месте 100 мл. дегтя эти 100 мл меда.

Значит, дегтя в мёде ровно столько же, сколько меда в дегте.

1)На Поле Чудес растут два дерева. Если закопать несколько золотых под одним из них, то наутро сумма удвоится, а если под вторым — утроится. У Буратино есть 100 золотых. Он не знает, какое из деревьев удваивает деньги, а какое утраивает, но хочет к утру иметь ровно 175 золотых. Как ему этого добиться? (Буратино может закопать часть денег под первое дерево, часть под второе, а часть не закапывать вовсе.)

Решение:

Пусть мы закопали 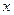монет под первым деревом и 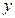под вторым (и еще оставили ; 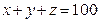). Тогда у нас будет 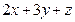или 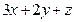к утру. Оба этих числа должны быть равны 175. Значит 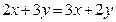; перенесем 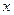вправо со сменой знака а 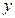влево. Получим 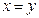. Тогда закопали 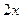монет, а получили к утру вместо них 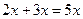. Profit! равный 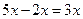. По условию должно получиться на 75 монет больше. .

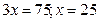Ответ: Нужно закопать под каждым деревом по 25 монет, остальные 50 не трогать.

2) Есть 100 пуговиц с двумя дырками и 100 пуговиц с четырьмя дырками. Можно ли положить их в 4 ящика стола, показанного на рисунке, так, чтобы в двух верхних ящиках лежало 120 пуговиц, в ящиках правой тумбы лежало 110 пуговиц, у пуговиц в двух нижних ящиках было бы в сумме 360 дырок и, наконец, у пуговиц в ящиках левой тумбы было бы 320 дырок? (К. Кохась)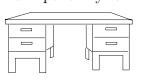

Решение:

Предположим, что нам удалось так разложить пуговицы. Тогда в двух нижних ящиках 360 дырок, значит не меньше 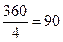пуговиц (так как в каждой пуговице не больше 4 дырок). И еще в двух верхних ящиках 120пуговиц. Всего не меньше 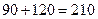пуговиц, противоречие.

Ответ: нельзя.

3) Привести пример трехзначного числа, которое не делится на 102, но если его записать 15 раз слитно, то получится 45-значное число, которое делится на 102.

Решение:

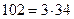. Если искомое трехзначное число делится на 34, то и полученное 45-значное тоже.

Поскольку числа 3 и 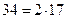взаимно просты (то есть не имеют общих делителей больших 1), число делится на 102 тогда и только тогда, когда оно делится на 34 и на 3. Признак делимости на 3: число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Но если у исходного числа сумма цифр 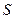, то у написанного она 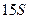и делится на 3. Значит, подойдет любое трехзначное число, которое делится на 34, но не делится на 102. Например, 170.

4)Котенок и щенок едят вместе сосиску таким методом: сперва котенок откусывает слева четверть сосиски. Затем щенок откусывает справа треть оставшейся части. Потом снова котенок слева четверть оставшейся части, затем щенок справа треть оставшекйся и так далее. Можно ли нанести отметку на сосиске так, чтобы котенок всегда ел только слева от метки, а щенок только справа?

Решение:

Пусть длина сосиски 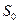. Котенок откусил 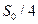, осталось 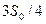.Затем щенок откусил

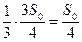и осталось 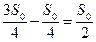. Обозначим это за 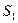. Дальше все аналогично, только индекс измениться с 0 на 1 и остаток обозначим 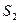и так далее. Видим, что каждый раз щенок откусывает ровно столько же, сколько и котенок. Значит, можно нанести отметку посередине и щенок будет кусать справа, а котенок слева.

5)(для сильных духом). Котенок ест сосиску следующим оригинальным методом. Сперва съедает среднюю треть сосиски (включая концы). Затем в каждой из оставшихся (2) частей он съедает среднюю треть (включая концы). Затем в каждой из оставшихся (4) частей он снова съедает среднюю треть и так далее. Можно ли отметить на сосисе точку так, чтобы котенок никогда не её не съел? (осторожно, эта задача может сломать детскую психику).

Решение:

Рассмотрим точку 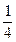. Она делит отрезок в отношении 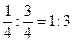. Посмотрим, на каком из оставшихся отрезкв она будет, и в каком отношении его поделит.Будет в левом отрезке. Слева 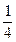, справа осталось 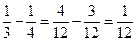. Значит та же точка 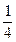делит оставшийся отрезок в отношении 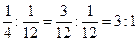. То есть в таком же отношении, только теперь справа налево если считать. Можно это представить, что отношение, в котором точка делит отрезок не изменилось, просто он перевернулся и уменьшился в 3 раза. Аналогично, в следующем оставшемся меньшем отрезке (уже длиной 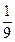) та же точка 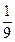снова будет делить его в отношении 1:3 и так далее, так для каждого следующего меньшего отрезка. Значит, котенок никогда не съест эту точку.

6) У Буратино и Пьеро был велосипед, на котором они отправились в соседнюю деревню. Ехали по очереди, но всякий раз, когда один ехал, другой шёл пешком, а не бежал. При этом они ухитрились прибыть в деревню почти в 2 раза быстрее, чем если бы оба шли пешком. Как им это удалось?

Решение:

Буратино проехал половину пути на велосипеде (а Пьеро в это время шел пешком). Затем Буратино бросил велосипед и пошел пешком. Пьеро через некоторое время подобрал велосипед и поехал на нем. Каждый из них проехал половину пути на велосипеде и половину прошел пешком. Если ездили на велосипеде они намного быстрее, чем шли пешком, получилось почти вдвое быстрее (так как пешком шли вдвое меньше). Докажем, что они не могли оба добраться до деревни еще быстрее (чем этим способом). Действительно, велосипед нет смысла возвращать назад. Значит, вместе они могла проехать на велосипеде в сумме не больше чем расстояние между деревнями. Значит, в сумме он прошли тоже не меньше чем расстояние между деревнями (так как на велосипеде + пешком они прошли удвоенное это расстояние в сумме). Если каждый проедет на велосипеде ровно половину расстояния (и половину соответственно пешком), получится то же время что и в предложенном способе. Если один из них проедет больше половины расстоянии на велосипеде, то второй проедет меньше половины и пройдет пешком больше половины расстояния. Значит, он прибудет позже чем в предложенном способе. И значит вместе они придут позже (так как время считается по последнему пришедшему)

7) Андрей, Боря и Коля участвовали в забеге. Когда Андрей финишировал, Боря отставал на 15 метров, а Коля на 35. После финиша Бори, Коле оставалось добежать 22 метра. Мальчики бежали всю дистанцию с постоянной скоростью. Какова длина дистанции?

Решение:

Андрей бежал быстрее Бори, а тот быстрее Коли. Скорость Бори относительно Коли постоянна (и равна разности их скоростей).К моменту финиша Андрея Боря обогнал Колю на 35-15=20 метров. А к моменту Финиша Бори на 22 метра, то есть пока Боря Бежал 15 метров он еще дополнительно оторвался от Коли на 22-20=2 метра. Что в 10 раз меньше, чем до финиша Андрея. Значит, до финиша Андрея прошло в 10 раз больше времени, чем от финиша Андрея до финиша Бори. Значит, за это время Боря пробежал 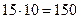метров. И длина дистанции 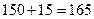метров

8) На Олимпиаде в Индии, которую проводил Маугли, в забегах приняли участие все животные - и жалкие дождевые черви, и вожак стаи старый Акелла, и даже злобный Шер-Хан. Их оказалось очень много - ровно 1 миллиард. Все животные получили последовательные номера от единицы и до одного миллиарда.

После первого забега победили участники у которых были нечетные номера, их заново пронумеровали - 1-й сохранил свой номер, участник с номером 3-й номер стал 2-м, с номером 5 - стал 3-м и так далее, проигравшие выбыли из соревнования.

Во втором забеге победили все участники, которые имели четные номера, их также заново пронумеровали: 2-й стал 1-м, 4-й - 2-м, 6-й - 3-м и так далее.

Как потом выяснилось, и далее в нечетных забегах побеждали участники с нечетными номерами, а в четных - с четными, и каждый раз после очередного забега участников перенумеровывали по той же схеме.

В конце концов победила хитрая Багира. Выясните какой у нее был номер в начале соревнований? (можно решить вариант этой задачи попроще с 1 миллион участников вместо 1 млрд. )

Решение:

Решим задачу для 1000 участников, для миллиона или миллиарда аналогично.

Каждый раз число участников либо уменьшалось в 2 раза (если получалось нецелое число, округляли в большую сторону). Поскольку 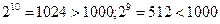, всего было 10 забегов. В последнем 10 забеге номер Багиры был 2 (так как 10 четное, из 1 и 2 победил 2).

В 9 забеге номер Багиры был 2 нечетным числом по порядку, то есть 3. В 8 забеге 3 по порядку четным числом, то есть 6 и так далее. Последовательно то умножаем на 2, вычитаем 1, если нечетный тур, то умножаем на 2, если четный. Получаем:

забег
Номер Багиры

Для миллиарда делается аналогично, но долго.