Выпуклость и вогнутость кривой. Точки перегиба.

Выпуклость и вогнутость кривой. Точки перегиба.

Рассмотрим на плоскости кривую, которая является графиком дифференцируемой функции .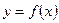

Определение 1.Кривая обращена выпуклостью вверх на интервале 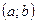, если все точки кривой лежат ниже любой её касательной на этом интервале.

Кривая обращена выпуклостью вниз на интервале 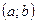, если все точки кривой лежат выше любой её касательной на этом интервале.

Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращённую выпуклостью вниз – вогнутой.

Теорема 1. Если во всех точках интервала 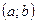вторая производная функции 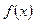отрицательна, т.е. 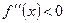, то кривая 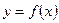обращена выпуклостью вверх (кривая выпукла).

Теорема 2. Если во всех точках интервала 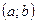вторая производная функции 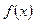положительна, т.е. 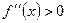, то кривая 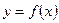обращена выпуклостью вниз (кривая вогнута).

Определение 2. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой.

В точке перегиба касательная пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Теорема 3 (необходимое условие точки перегиба). Для того чтобы график функции 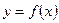имел перегиб в точке 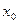, необходимо, чтобы функция была дифференцируема в точке 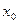, и чтобы в этой точке вторая производная либо не существовала, либо была равна нулю.

Теорема 4 (достаточное условие точки перегиба).Пусть кривая определяется уравнением 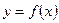. Ес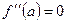ли или 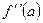не существует и при переходе через точку 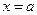производная 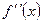меняет знак, то точка кривой с абсциссой 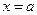есть точка перегиба.

Пример: Найдите точки экстремума и точки перегиба функции .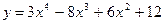

Решение. Находим область определения функции: .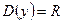

Первая производная функции равна:

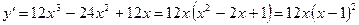Приравняем производную к нулю и найдем критические точки: 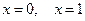. При переходе через точку 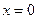производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. При переходе через точку 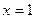производная не меняет знака, следовательно, в этой точке функция не имеет экстремума.

Найдём значение функции в точке минимума .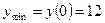

Вторая производная функции равна:

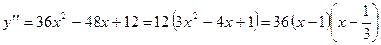Приравняем вторую производную к нулю и найдем точки: . При переходе через эти точки производная меняет знак, следовательно, они являются точками перегиба.

Найдём значения функции в точках перегиба: , .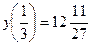

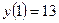Результаты исследования сведены в таблицу:

x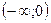
	-	+	+
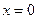
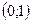
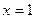
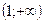
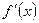
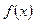
	убывает	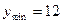Возрастает	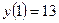Возрастает
x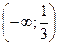
	+	-	+
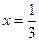
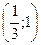
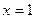
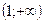
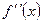
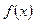
	вогнутость	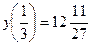выпуклость	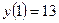Вогнутость