Уважаемые студенты гр. ТО-203к прошу выполненные задания и последующие, делать

Уважаемые студенты гр. ТО-203к прошу выполненные задания и последующие, делать

Скриншоты (фотоотчеты) и присылать на страничку в контакте https://vk.com/id356059967 Татьяна Сафонова указывая название предмета, группу, фамилию, имя, отчество.

Выполнить практическую работу №3 по примеру, взяв свой вариант по списку.

	Анисимов П. С.
	Агарков А.В.
	Борисов Д. И.
	Баскаков Д. А.
	Вобленко А. А.
	Выставкин К. А.
	Грибанов А. С.
	Данилов В. М.
	Данилов Д. А.
	Демидюк И. Л.
	Золотарев М.С.
	Зуев С.А.
	Иванов Н. А.
	Кабанов Р.А.
	Кипуров А. С.
	Кузнецов А. В.
	Кузьмин М. Е.
18	Леонов Д. А.
	Менделев Г. И.
20	Неупокоев Д. А.
21	Рыжиков Д.Д.

Практическое занятие №3

Тема:Определение центра тяжести плоских фигур и сечений

Цель: Научиться определению центра тяжести плоских фигур и сечений

Теоретическая часть

Центр тяжести

Сила тяжести – равнодействующая сил притяжения к Земле, распределённых по всему объему тела.

Центр тяжести тела– это такая неизменно связанная с этим телом точка, через которую проходит линия действия силы тяжести данного тела при любом положении тела в пространстве.

Методы нахождения центра тяжести

1. Метод симметрии:

1.1. Если однородное тело имеет плоскость симметрии, то центр тяжести лежит в этой плоскости

1.2. Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси. Центр тяжести однородного тела вращения лежит на оси вращения.

1.3 Если однородное тело имеет две оси симметрии, то центр тяжести находится в точке их пересечения.

2. Метод разбиения: Тело разбивается на наименьшее число частей, силы тяжести и положение центров тяжести которых известны.

3. Метод отрицательных масс: При определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но массу свободных полостей считать отрицательной.

Координаты центра тяжести плоской фигуры:

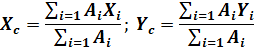
Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам. (рисунок 1.13)

Примечание:Центр тяжести симметрии фигуры находится на оси симметрии.

Центр тяжести стержня находится на середине высоты.

Пример:

Определите координаты центра тяжести плоской пластины, представленной на (рис.1) при известных геометрических параметрах.

Дано: В = 140 мм, b = 100мм,

      H = 120 мм, R = 30 мм деталь в виде плоской пластины.

Найти: X_C, Yc - координаты центра тяжести

Решение

1. Разбиваем деталь «плоскую пластину» на типовые геометрические фигуры и определяем их площади:



1 — прямоугольник,   А₁= H · b =120 · 100 = 12000 мм²;



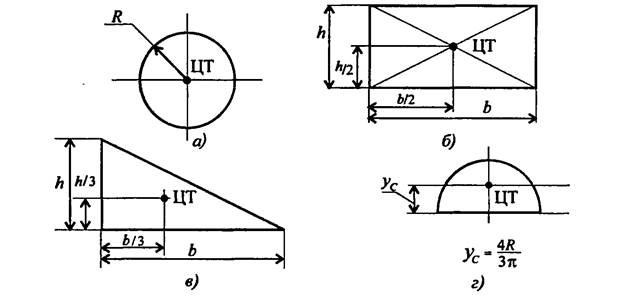
2 — треугольник,       ;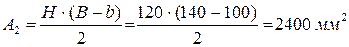



3 — полукруг,            .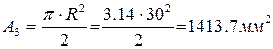

2. Определяем центр тяжести каждой фигуры, расположив ось координат в левый угол основания прямоугольника:

ЦТ фигуры 1: ;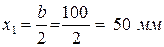

ЦТ фигуры 2:

ЦТ фигуры 3:

3. По типовой формуле определяем координаты центра тяжести пластины

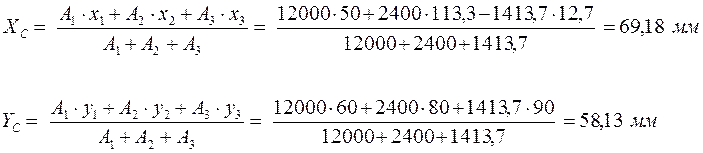Вывод:

Варианты заданий.

№ Вари анта B мм b мм H мм R мм № Вари анта B мм b мм H мм R мм

100 50 80 20 200 145 110 25

110 55 80 20 205 150 120 25

115 60 80 20 210 155 120 25

120 65 80 20 215 160 120 30

125 70 80 20 220 165 120 30

130 75 90 20 225 170 120 30

135 80 90 20 230 175 125 30

140 85 90 20 235 180 125 30

145 90 90 20 240 185 125 30

150 95 90 20 245 190 125 30

155 100 100 20 250 195 125 30

160 105 100 20 255 200 130 30

165 110 100 25 260 205 130 35

170 115 100 25 265 210 130 35

175 120 100 25 270 215 130 35

180 125 110 25 275 220 130 35

185 130 110 25 280 225 135 35

190 135 110 25 285 230 135 35

195 140 110 25 290 235 135 35